题目
设为3维单位列向量，矩阵，则的全部特征值为_____。
设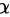
为3维单位列向量，矩阵
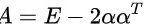，则
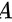的全部特征值为_____。
题目解答
答案
由已知有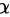：为3维单位列向量
设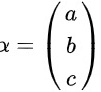
，其中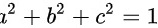
。
故矩阵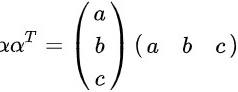
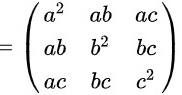
故矩阵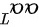
为实对称矩阵，且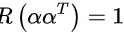
则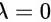
为矩阵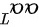的二重特征值
又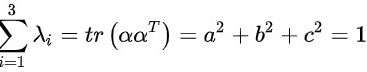
则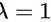
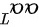为矩阵的特征值
矩阵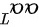的全部特征值为
。
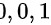故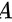的全部特征值为
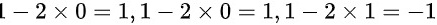，即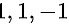
。
故答案为：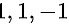
解析
步骤 1：确定矩阵$A$的结构
矩阵$A$由单位矩阵$E$减去$2\alpha {\alpha }^{T}$构成，其中$\alpha$是3维单位列向量。这意味着$\alpha$的长度为1，即${\alpha }^{T}\alpha =1$。
步骤 2：确定矩阵$A$的特征值
由于$\alpha$是单位列向量，矩阵$\alpha {\alpha }^{T}$的秩为1，因此矩阵$A$的秩为2。这意味着矩阵$A$有2个非零特征值和1个零特征值。由于$A$是对称矩阵，其特征值为实数。
步骤 3：计算特征值
矩阵$A$的迹（即对角线元素之和）等于$E$的迹减去$2\alpha {\alpha }^{T}$的迹。由于$E$的迹为3，而$2\alpha {\alpha }^{T}$的迹为$2{\alpha }^{T}\alpha =2$，因此$A$的迹为$3-2=1$。由于$A$的秩为2，其特征值中有一个为0，另外两个特征值之和为1。由于$A$是对称矩阵，其特征值为实数，因此这两个非零特征值为1和-1。
矩阵$A$由单位矩阵$E$减去$2\alpha {\alpha }^{T}$构成，其中$\alpha$是3维单位列向量。这意味着$\alpha$的长度为1，即${\alpha }^{T}\alpha =1$。
步骤 2：确定矩阵$A$的特征值
由于$\alpha$是单位列向量，矩阵$\alpha {\alpha }^{T}$的秩为1，因此矩阵$A$的秩为2。这意味着矩阵$A$有2个非零特征值和1个零特征值。由于$A$是对称矩阵，其特征值为实数。
步骤 3：计算特征值
矩阵$A$的迹（即对角线元素之和）等于$E$的迹减去$2\alpha {\alpha }^{T}$的迹。由于$E$的迹为3，而$2\alpha {\alpha }^{T}$的迹为$2{\alpha }^{T}\alpha =2$，因此$A$的迹为$3-2=1$。由于$A$的秩为2，其特征值中有一个为0，另外两个特征值之和为1。由于$A$是对称矩阵，其特征值为实数，因此这两个非零特征值为1和-1。