题目
已知 (alpha )_(1)=(1,2,-3), (alpha )_(2)=(2,-1,-1),(alpha )_(1)=(1,2,-3), (alpha )_(2)=(2,-1,-1),求该向量组的一极大无关组 并将其余向量用极大无关组表示 .
已知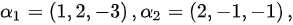 
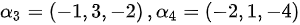求该向量组的一极大无关组 并将其余向量用极大无关组表示 .
题目解答
答案
极大无关组为：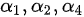
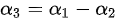
求解过程如下：
解：
设矩阵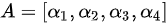
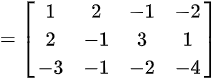，然后将矩阵化为行阶梯型：
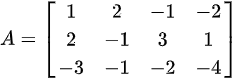
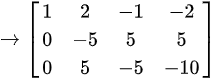（将第一行的-2倍加至第二行，第一行的3倍加至第三行）
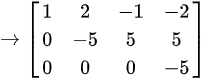（将第二行的1倍加至第三行）
（第二行每个元素都除以-5，第三行每个元素也除以-5）即得到行阶梯型矩阵。
∴取每行第一个非零元素所在列对应的向量即为极大无关组中的向量，即第一二四列对应的向量，
∴极大无关组为：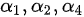
且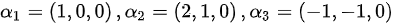
∴
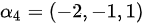
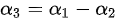
∴答案为：
极大无关组：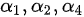
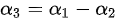
解析
步骤 1：构造矩阵
构造矩阵$A=[ {\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4}] $，即
$$
A=\begin{pmatrix}
1 & 2 & -1 & -2 \\
2 & -1 & 3 & 1 \\
-3 & -1 & -2 & -4
\end{pmatrix}
$$
步骤 2：化简为行阶梯型
将矩阵化为行阶梯型，即通过行变换使矩阵的每一行的第一个非零元素（主元）位于前一主元的右侧。
$$
\begin{pmatrix}
1 & 2 & -1 & -2 \\
2 & -1 & 3 & 1 \\
-3 & -1 & -2 & -4
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & -1 & -2 \\
0 & -5 & 5 & 5 \\
0 & 5 & -5 & -10
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & -1 & -2 \\
0 & -5 & 5 & 5 \\
0 & 0 & 0 & -5
\end{pmatrix}
$$
步骤 3：确定极大无关组
取每行第一个非零元素所在列对应的向量即为极大无关组中的向量，即第一二四列对应的向量。
步骤 4：表示其余向量
根据行阶梯型矩阵，可以表示出${\alpha }_{3}$为极大无关组中向量的线性组合。
构造矩阵$A=[ {\alpha }_{1},{\alpha }_{2},{\alpha }_{3},{\alpha }_{4}] $，即
$$
A=\begin{pmatrix}
1 & 2 & -1 & -2 \\
2 & -1 & 3 & 1 \\
-3 & -1 & -2 & -4
\end{pmatrix}
$$
步骤 2：化简为行阶梯型
将矩阵化为行阶梯型，即通过行变换使矩阵的每一行的第一个非零元素（主元）位于前一主元的右侧。
$$
\begin{pmatrix}
1 & 2 & -1 & -2 \\
2 & -1 & 3 & 1 \\
-3 & -1 & -2 & -4
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & -1 & -2 \\
0 & -5 & 5 & 5 \\
0 & 5 & -5 & -10
\end{pmatrix}
\rightarrow
\begin{pmatrix}
1 & 2 & -1 & -2 \\
0 & -5 & 5 & 5 \\
0 & 0 & 0 & -5
\end{pmatrix}
$$
步骤 3：确定极大无关组
取每行第一个非零元素所在列对应的向量即为极大无关组中的向量，即第一二四列对应的向量。
步骤 4：表示其余向量
根据行阶梯型矩阵，可以表示出${\alpha }_{3}$为极大无关组中向量的线性组合。