10.设周期为2π的函数f(x)在 [ -pi ,pi ] 上的Fourier系数为a,和bn,求下列函数的Fourier系数an-|||-和bn:-|||-(1) (x)=f(-x);-|||-(2) h(x)=f(x+C) (C是常数);-|||-(3) (x)=dfrac (1)(pi )(int )_(-pi )^nf(t)f(x-t)dt (假定积分顺序可以交换).

题目解答
答案
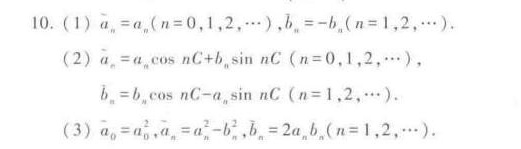
解析
考查要点:本题主要考查Fourier系数在函数对称、平移、卷积等变换下的变化规律,需要熟练掌握Fourier系数的定义及性质。
解题思路:
- 对称变换:通过变量代换,分析函数对称性对积分的影响;
- 平移变换:利用三角函数的加法公式展开平移后的表达式,重新组合系数;
- 卷积运算:结合Fourier系数的卷积定理,或直接展开积分计算。
关键点:
- 对称性:偶函数保留余弦项,奇函数保留正弦项;
- 平移性质:平移后系数涉及原系数与三角函数的线性组合;
- 卷积定理:卷积的Fourier系数等于原系数的乘积。
(1) $g(x) = f(-x)$
计算$a_n'$
$\begin{aligned}a_n' &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(-x) \cos(nx) \, dx \\&\underset{x=-y}{=} \frac{1}{\pi} \int_{-\pi}^{\pi} f(y) \cos(ny) \, dy = a_n\end{aligned}$
计算$b_n'$
$\begin{aligned}b_n' &= \frac{1}{\pi} \int_{-\pi}^{\pi} f(-x) \sin(nx) \, dx \\&\underset{x=-y}{=} \frac{1}{\pi} \int_{-\pi}^{\pi} f(y) (-\sin(ny)) \, dy = -b_n\end{aligned}$
(2) $h(x) = f(x + C)$
展开平移后的函数
$h(x) = \sum_{n=0}^{\infty} a_n \cos(n(x+C)) + \sum_{n=1}^{\infty} b_n \sin(n(x+C))$
利用三角恒等式
$\begin{aligned}\cos(n(x+C)) &= \cos(nx)\cos(nC) - \sin(nx)\sin(nC), \\\sin(n(x+C)) &= \sin(nx)\cos(nC) + \cos(nx)\sin(nC)\end{aligned}$
重新组合系数
$\begin{aligned}a_n' &= a_n \cos(nC) + b_n \sin(nC), \\b_n' &= b_n \cos(nC) - a_n \sin(nC)\end{aligned}$
(3) $F(x) = \frac{1}{\pi} \int_{-\pi}^{\pi} f(t)f(x-t) \, dt$
利用卷积定理
$\hat{a}_n = a_n^2 - b_n^2, \quad \hat{b}_n = 2a_n b_n \quad (n \geq 1), \quad \hat{a}_0 = a_0^2$