题目
(2)函数 (x)=dfrac ({x)^2-x}({x)^2-1}sqrt (1+dfrac {1)({x)^2}} 的无穷间断点的个数为 ()-|||-(A)0 (B) 1 (C)2 (D) 3

题目解答
答案
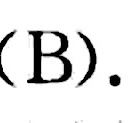
解析
步骤 1:确定函数的定义域
函数 $f(x)=\dfrac {{x}^{2}-x}{{x}^{2}-1}\sqrt {1+\dfrac {1}{{x}^{2}}}$ 的定义域为所有使得分母不为零的实数 $x$,即 $x^2 - 1 \neq 0$。因此,$x \neq \pm 1$。同时,根号内的表达式 $1 + \dfrac{1}{x^2}$ 总是非负的,所以根号内的表达式不会影响定义域。
步骤 2:分析无穷间断点
无穷间断点是指函数在某点的极限为无穷大或无穷小。对于函数 $f(x)$,我们需要检查 $x = \pm 1$ 处的极限情况。
- 当 $x \to 1$ 时,$f(x) = \dfrac {1-x}{(1-x)(1+x)}\sqrt {1+\dfrac {1}{x^2}} = \dfrac {1}{1+x}\sqrt {1+\dfrac {1}{x^2}}$。由于 $x \to 1$ 时,$1+x \to 2$,$\sqrt {1+\dfrac {1}{x^2}} \to \sqrt{2}$,所以 $f(x) \to \dfrac{\sqrt{2}}{2}$,不是无穷大或无穷小。
- 当 $x \to -1$ 时,$f(x) = \dfrac {1-x}{(1-x)(1+x)}\sqrt {1+\dfrac {1}{x^2}} = \dfrac {1}{1+x}\sqrt {1+\dfrac {1}{x^2}}$。由于 $x \to -1$ 时,$1+x \to 0$,$\sqrt {1+\dfrac {1}{x^2}} \to \sqrt{2}$,所以 $f(x) \to \infty$,是无穷大。
步骤 3:总结无穷间断点的个数
根据上述分析,函数 $f(x)$ 在 $x = -1$ 处有一个无穷间断点,而在 $x = 1$ 处没有无穷间断点。
函数 $f(x)=\dfrac {{x}^{2}-x}{{x}^{2}-1}\sqrt {1+\dfrac {1}{{x}^{2}}}$ 的定义域为所有使得分母不为零的实数 $x$,即 $x^2 - 1 \neq 0$。因此,$x \neq \pm 1$。同时,根号内的表达式 $1 + \dfrac{1}{x^2}$ 总是非负的,所以根号内的表达式不会影响定义域。
步骤 2:分析无穷间断点
无穷间断点是指函数在某点的极限为无穷大或无穷小。对于函数 $f(x)$,我们需要检查 $x = \pm 1$ 处的极限情况。
- 当 $x \to 1$ 时,$f(x) = \dfrac {1-x}{(1-x)(1+x)}\sqrt {1+\dfrac {1}{x^2}} = \dfrac {1}{1+x}\sqrt {1+\dfrac {1}{x^2}}$。由于 $x \to 1$ 时,$1+x \to 2$,$\sqrt {1+\dfrac {1}{x^2}} \to \sqrt{2}$,所以 $f(x) \to \dfrac{\sqrt{2}}{2}$,不是无穷大或无穷小。
- 当 $x \to -1$ 时,$f(x) = \dfrac {1-x}{(1-x)(1+x)}\sqrt {1+\dfrac {1}{x^2}} = \dfrac {1}{1+x}\sqrt {1+\dfrac {1}{x^2}}$。由于 $x \to -1$ 时,$1+x \to 0$,$\sqrt {1+\dfrac {1}{x^2}} \to \sqrt{2}$,所以 $f(x) \to \infty$,是无穷大。
步骤 3:总结无穷间断点的个数
根据上述分析,函数 $f(x)$ 在 $x = -1$ 处有一个无穷间断点,而在 $x = 1$ 处没有无穷间断点。