题目
若D是=(x)^2 =1和x轴所围成的位于第一象限的平面区域,计算二重积分=(x)^2 =1
若D是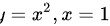
和x轴所围成的位于第一象限的平面区域,计算二重积分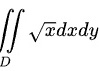
题目解答
答案
由题可得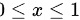
,
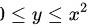
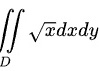
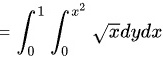
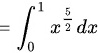
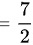
解析
步骤 1：确定积分区域
根据题目描述，积分区域D由曲线$y=x^2$，直线$x=1$和x轴在第一象限围成。因此，积分区域D的边界为$0\leqslant x\leqslant 1$和$0\leqslant y\leqslant x^2$。
步骤 2：设置二重积分
根据题目要求，需要计算二重积分$\iint_{D}\sqrt{x}dxdy$。根据步骤1中确定的积分区域，可以将二重积分表示为$\int_{0}^{1}\int_{0}^{x^2}\sqrt{x}dydx$。
步骤 3：计算二重积分
首先，计算内层积分$\int_{0}^{x^2}\sqrt{x}dy$。由于$\sqrt{x}$是关于y的常数，因此内层积分的结果为$\sqrt{x}\int_{0}^{x^2}dy=\sqrt{x}y|_{0}^{x^2}=\sqrt{x}x^2$。
然后，计算外层积分$\int_{0}^{1}\sqrt{x}x^2dx$。将$\sqrt{x}x^2$表示为$x^{5/2}$，则外层积分变为$\int_{0}^{1}x^{5/2}dx$。根据幂函数的积分公式，$\int x^n dx = \frac{x^{n+1}}{n+1} + C$，可以得到$\int_{0}^{1}x^{5/2}dx = \frac{x^{7/2}}{7/2}|_{0}^{1} = \frac{2}{7}x^{7/2}|_{0}^{1} = \frac{2}{7}$。
根据题目描述，积分区域D由曲线$y=x^2$，直线$x=1$和x轴在第一象限围成。因此，积分区域D的边界为$0\leqslant x\leqslant 1$和$0\leqslant y\leqslant x^2$。
步骤 2：设置二重积分
根据题目要求，需要计算二重积分$\iint_{D}\sqrt{x}dxdy$。根据步骤1中确定的积分区域，可以将二重积分表示为$\int_{0}^{1}\int_{0}^{x^2}\sqrt{x}dydx$。
步骤 3：计算二重积分
首先，计算内层积分$\int_{0}^{x^2}\sqrt{x}dy$。由于$\sqrt{x}$是关于y的常数，因此内层积分的结果为$\sqrt{x}\int_{0}^{x^2}dy=\sqrt{x}y|_{0}^{x^2}=\sqrt{x}x^2$。
然后，计算外层积分$\int_{0}^{1}\sqrt{x}x^2dx$。将$\sqrt{x}x^2$表示为$x^{5/2}$，则外层积分变为$\int_{0}^{1}x^{5/2}dx$。根据幂函数的积分公式，$\int x^n dx = \frac{x^{n+1}}{n+1} + C$，可以得到$\int_{0}^{1}x^{5/2}dx = \frac{x^{7/2}}{7/2}|_{0}^{1} = \frac{2}{7}x^{7/2}|_{0}^{1} = \frac{2}{7}$。