题目
23.设二维随机变量(X,Y)的联合概率密度为-|||-f(x,y)= { 的概率密度函数.

题目解答
答案
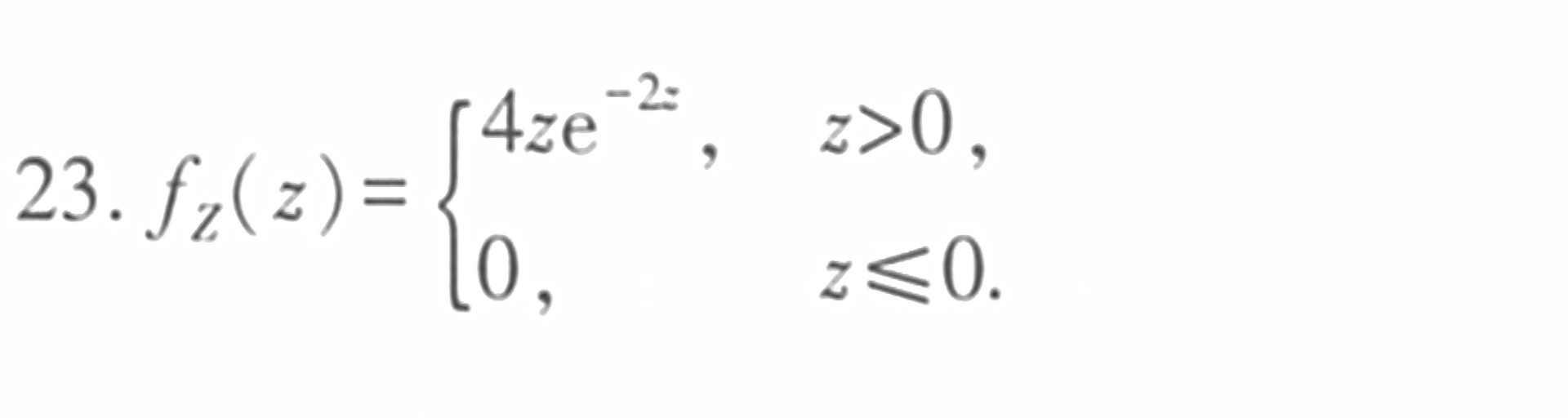
解析
步骤 1:确定 $Z$ 的取值范围
由于 $X>0$ 和 $Y>0$,则 $Z=\dfrac {X+Y}{2}>0$。因此,$Z$ 的取值范围为 $(0,+\infty)$。
步骤 2:求 $Z$ 的分布函数
$Z$ 的分布函数 $F_Z(z)$ 定义为 $F_Z(z)=P(Z\leqslant z)$。由于 $Z=\dfrac {X+Y}{2}$,则 $F_Z(z)=P(\dfrac {X+Y}{2}\leqslant z)=P(X+Y\leqslant 2z)$。因此,$F_Z(z)$ 可以表示为 $F_Z(z)=\int _{0}^{2z}\int _{0}^{2z-y}f(x,y)dxdy$,其中 $f(x,y)$ 是 $X$ 和 $Y$ 的联合概率密度函数。
步骤 3:计算 $F_Z(z)$
根据 $f(x,y)$ 的定义,$F_Z(z)=\int _{0}^{2z}\int _{0}^{2z-y}{e}^{-(x+y)}dxdy$。计算该积分,得到 $F_Z(z)=1-{e}^{-2z}-2z{e}^{-2z}$。
步骤 4:求 $Z$ 的概率密度函数
$Z$ 的概率密度函数 $f_Z(z)$ 是 $F_Z(z)$ 的导数,即 $f_Z(z)=\dfrac {d}{dz}F_Z(z)$。计算该导数,得到 $f_Z(z)=4z{e}^{-2z}$,其中 $z>0$。
由于 $X>0$ 和 $Y>0$,则 $Z=\dfrac {X+Y}{2}>0$。因此,$Z$ 的取值范围为 $(0,+\infty)$。
步骤 2:求 $Z$ 的分布函数
$Z$ 的分布函数 $F_Z(z)$ 定义为 $F_Z(z)=P(Z\leqslant z)$。由于 $Z=\dfrac {X+Y}{2}$,则 $F_Z(z)=P(\dfrac {X+Y}{2}\leqslant z)=P(X+Y\leqslant 2z)$。因此,$F_Z(z)$ 可以表示为 $F_Z(z)=\int _{0}^{2z}\int _{0}^{2z-y}f(x,y)dxdy$,其中 $f(x,y)$ 是 $X$ 和 $Y$ 的联合概率密度函数。
步骤 3:计算 $F_Z(z)$
根据 $f(x,y)$ 的定义,$F_Z(z)=\int _{0}^{2z}\int _{0}^{2z-y}{e}^{-(x+y)}dxdy$。计算该积分,得到 $F_Z(z)=1-{e}^{-2z}-2z{e}^{-2z}$。
步骤 4:求 $Z$ 的概率密度函数
$Z$ 的概率密度函数 $f_Z(z)$ 是 $F_Z(z)$ 的导数,即 $f_Z(z)=\dfrac {d}{dz}F_Z(z)$。计算该导数,得到 $f_Z(z)=4z{e}^{-2z}$,其中 $z>0$。