int dfrac (2{x)^2-x-1}({x)^3+1}dx.
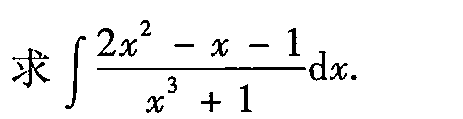
题目解答
答案

解析
考查要点:本题主要考查有理分式的积分方法,特别是部分分式分解、代数变形以及积分技巧的综合应用。
解题核心思路:
- 分母因式分解:将分母$x^3 + 1$分解为$(x + 1)(x^2 - x + 1)$。
- 部分分式分解:将原分式拆分为$\frac{A}{x + 1} + \frac{Bx + C}{x^2 - x + 1}$的形式,通过待定系数法求解$A, B, C$。
- 分项积分:分别对拆分后的两部分积分,其中第二部分需通过分子变形转化为标准积分形式(对数积分和反正切积分)。
破题关键点:
- 分子变形:将分子$4x - 5$拆分为$2(2x - 1) - 3$,使得积分可分解为导数项和常数项。
- 完成平方:将二次分母$x^2 - x + 1$转化为$(x - \frac{1}{2})^2 + \frac{3}{4}$,便于应用反正切积分公式。
步骤1:分母因式分解
将分母$x^3 + 1$分解为:
$x^3 + 1 = (x + 1)(x^2 - x + 1)$
步骤2:部分分式分解
设原分式可分解为:
$\frac{2x^2 - x - 1}{(x + 1)(x^2 - x + 1)} = \frac{A}{x + 1} + \frac{Bx + C}{x^2 - x + 1}$
通过通分并比较系数,解得:
$A = \frac{2}{3}, \quad B = \frac{4}{3}, \quad C = -\frac{5}{3}$
因此,原积分可拆分为:
$\int \frac{2}{3(x + 1)} \, dx + \int \frac{4x - 5}{3(x^2 - x + 1)} \, dx$
步骤3:分项积分
-
第一部分积分:
$\int \frac{2}{3(x + 1)} \, dx = \frac{2}{3} \ln |x + 1| + C_1$ -
第二部分积分:
将分子$4x - 5$变形为$2(2x - 1) - 3$,拆分为两部分:
$\int \frac{4x - 5}{3(x^2 - x + 1)} \, dx = \frac{2}{3} \int \frac{2x - 1}{x^2 - x + 1} \, dx - \frac{3}{3} \int \frac{1}{x^2 - x + 1} \, dx$
-
第一部分:
$\frac{2}{3} \int \frac{2x - 1}{x^2 - x + 1} \, dx = \frac{2}{3} \ln |x^2 - x + 1| + C_2$ -
第二部分:
将分母完成平方:
$x^2 - x + 1 = \left(x - \frac{1}{2}\right)^2 + \frac{3}{4}$
积分结果为:
$-\int \frac{1}{\left(x - \frac{1}{2}\right)^2 + \left(\frac{\sqrt{3}}{2}\right)^2} \, dx = -\frac{2}{\sqrt{3}} \arctan \left(\frac{2x - 1}{\sqrt{3}}\right) + C_3$
步骤4:合并结果
综合所有部分,最终结果为:
$\frac{2}{3} \ln |x + 1| + \frac{2}{3} \ln |x^2 - x + 1| - \frac{2}{\sqrt{3}} \arctan \left(\frac{2x - 1}{\sqrt{3}}\right) + C$
进一步合并对数项:
$\frac{2}{3} \ln |x^3 + 1| - \frac{2}{\sqrt{3}} \arctan \left(\frac{2x - 1}{\sqrt{3}}\right) + C$