题目
22.设二维随机变量(X,Y)的概率密度-|||-f(x,y)= ) x+y,0leqslant xleqslant 1,0leqslant yleqslant 1 0 .-|||-求EX,EY,DX,DY,E(XY),cov(X,Y)及ρXY·

题目解答
答案
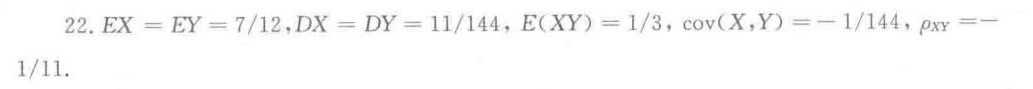
解析
步骤 1:计算EX
EX = $\int_{0}^{1}\int_{0}^{1} x(x+y) \, dy \, dx$ = $\int_{0}^{1} x \left( \int_{0}^{1} (x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x \left( x + \frac{1}{2} \right) \, dx$ = $\frac{7}{12}$
步骤 2:计算EY
EY = $\int_{0}^{1}\int_{0}^{1} y(x+y) \, dy \, dx$ = $\int_{0}^{1} \left( \int_{0}^{1} y(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} \left( \frac{1}{2}x + \frac{1}{3} \right) \, dx$ = $\frac{7}{12}$
步骤 3:计算DX
DX = E(X^2) - (EX)^2
E(X^2) = $\int_{0}^{1}\int_{0}^{1} x^2(x+y) \, dy \, dx$ = $\int_{0}^{1} x^2 \left( \int_{0}^{1} (x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x^2 \left( x + \frac{1}{2} \right) \, dx$ = $\frac{11}{12}$
DX = $\frac{11}{12} - \left( \frac{7}{12} \right)^2$ = $\frac{11}{144}$
步骤 4:计算DY
DY = E(Y^2) - (EY)^2
E(Y^2) = $\int_{0}^{1}\int_{0}^{1} y^2(x+y) \, dy \, dx$ = $\int_{0}^{1} \left( \int_{0}^{1} y^2(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} \left( \frac{1}{3}x + \frac{1}{4} \right) \, dx$ = $\frac{11}{12}$
DY = $\frac{11}{12} - \left( \frac{7}{12} \right)^2$ = $\frac{11}{144}$
步骤 5:计算E(XY)
E(XY) = $\int_{0}^{1}\int_{0}^{1} xy(x+y) \, dy \, dx$ = $\int_{0}^{1} x \left( \int_{0}^{1} y(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x \left( \frac{1}{2}x + \frac{1}{3} \right) \, dx$ = $\frac{1}{3}$
步骤 6:计算cov(X,Y)
cov(X,Y) = E(XY) - EXEY = $\frac{1}{3} - \left( \frac{7}{12} \right)^2$ = $-\frac{1}{144}$
步骤 7:计算ρXY
ρXY = $\frac{cov(X,Y)}{\sqrt{DX} \sqrt{DY}}$ = $\frac{-\frac{1}{144}}{\sqrt{\frac{11}{144}} \sqrt{\frac{11}{144}}}$ = $-\frac{1}{11}$
EX = $\int_{0}^{1}\int_{0}^{1} x(x+y) \, dy \, dx$ = $\int_{0}^{1} x \left( \int_{0}^{1} (x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x \left( x + \frac{1}{2} \right) \, dx$ = $\frac{7}{12}$
步骤 2:计算EY
EY = $\int_{0}^{1}\int_{0}^{1} y(x+y) \, dy \, dx$ = $\int_{0}^{1} \left( \int_{0}^{1} y(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} \left( \frac{1}{2}x + \frac{1}{3} \right) \, dx$ = $\frac{7}{12}$
步骤 3:计算DX
DX = E(X^2) - (EX)^2
E(X^2) = $\int_{0}^{1}\int_{0}^{1} x^2(x+y) \, dy \, dx$ = $\int_{0}^{1} x^2 \left( \int_{0}^{1} (x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x^2 \left( x + \frac{1}{2} \right) \, dx$ = $\frac{11}{12}$
DX = $\frac{11}{12} - \left( \frac{7}{12} \right)^2$ = $\frac{11}{144}$
步骤 4:计算DY
DY = E(Y^2) - (EY)^2
E(Y^2) = $\int_{0}^{1}\int_{0}^{1} y^2(x+y) \, dy \, dx$ = $\int_{0}^{1} \left( \int_{0}^{1} y^2(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} \left( \frac{1}{3}x + \frac{1}{4} \right) \, dx$ = $\frac{11}{12}$
DY = $\frac{11}{12} - \left( \frac{7}{12} \right)^2$ = $\frac{11}{144}$
步骤 5:计算E(XY)
E(XY) = $\int_{0}^{1}\int_{0}^{1} xy(x+y) \, dy \, dx$ = $\int_{0}^{1} x \left( \int_{0}^{1} y(x+y) \, dy \right) \, dx$ = $\int_{0}^{1} x \left( \frac{1}{2}x + \frac{1}{3} \right) \, dx$ = $\frac{1}{3}$
步骤 6:计算cov(X,Y)
cov(X,Y) = E(XY) - EXEY = $\frac{1}{3} - \left( \frac{7}{12} \right)^2$ = $-\frac{1}{144}$
步骤 7:计算ρXY
ρXY = $\frac{cov(X,Y)}{\sqrt{DX} \sqrt{DY}}$ = $\frac{-\frac{1}{144}}{\sqrt{\frac{11}{144}} \sqrt{\frac{11}{144}}}$ = $-\frac{1}{11}$