题目
求下列极限:-|||-lim _(narrow infty )(3)^nsin dfrac (x)({3)^n} _
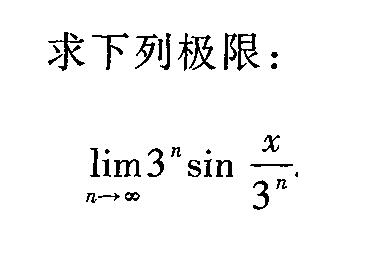
题目解答
答案
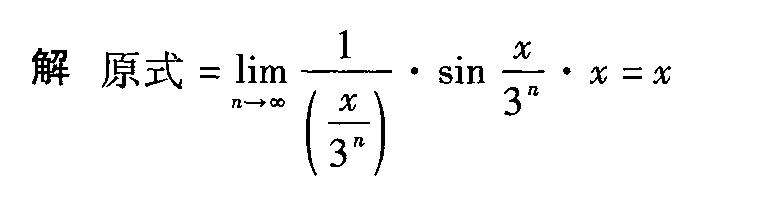
解析
步骤 1:转换极限形式
将原极限表达式 $\lim _{n\rightarrow \infty }{3}^{n}\sin \dfrac {x}{{3}^{n}}$ 转换为 $\lim _{n\rightarrow \infty }\dfrac {1}{(\dfrac {x}{{3}^{n}})}\cdot \sin \dfrac {x}{{3}^{n}}\cdot x$,这样可以利用 $\lim _{u\rightarrow 0}\dfrac {\sin u}{u} = 1$ 的性质。
步骤 2:应用极限性质
当 $n\rightarrow \infty$ 时,$\dfrac {x}{{3}^{n}}\rightarrow 0$,因此 $\lim _{n\rightarrow \infty }\dfrac {\sin \dfrac {x}{{3}^{n}}}{\dfrac {x}{{3}^{n}}} = 1$。
步骤 3:计算最终结果
将步骤 2 的结果代入步骤 1 的表达式中,得到 $\lim _{n\rightarrow \infty }{3}^{n}\sin \dfrac {x}{{3}^{n}} = \lim _{n\rightarrow \infty }\dfrac {1}{(\dfrac {x}{{3}^{n}})}\cdot \sin \dfrac {x}{{3}^{n}}\cdot x = 1 \cdot x = x$。
将原极限表达式 $\lim _{n\rightarrow \infty }{3}^{n}\sin \dfrac {x}{{3}^{n}}$ 转换为 $\lim _{n\rightarrow \infty }\dfrac {1}{(\dfrac {x}{{3}^{n}})}\cdot \sin \dfrac {x}{{3}^{n}}\cdot x$,这样可以利用 $\lim _{u\rightarrow 0}\dfrac {\sin u}{u} = 1$ 的性质。
步骤 2:应用极限性质
当 $n\rightarrow \infty$ 时,$\dfrac {x}{{3}^{n}}\rightarrow 0$,因此 $\lim _{n\rightarrow \infty }\dfrac {\sin \dfrac {x}{{3}^{n}}}{\dfrac {x}{{3}^{n}}} = 1$。
步骤 3:计算最终结果
将步骤 2 的结果代入步骤 1 的表达式中,得到 $\lim _{n\rightarrow \infty }{3}^{n}\sin \dfrac {x}{{3}^{n}} = \lim _{n\rightarrow \infty }\dfrac {1}{(\dfrac {x}{{3}^{n}})}\cdot \sin \dfrac {x}{{3}^{n}}\cdot x = 1 \cdot x = x$。