题目
极限 lim _(xarrow 0)dfrac ({(2+cos x))^x-(3)^x}((1-sqrt {1-{x)^2})ln (1+} 为() ()
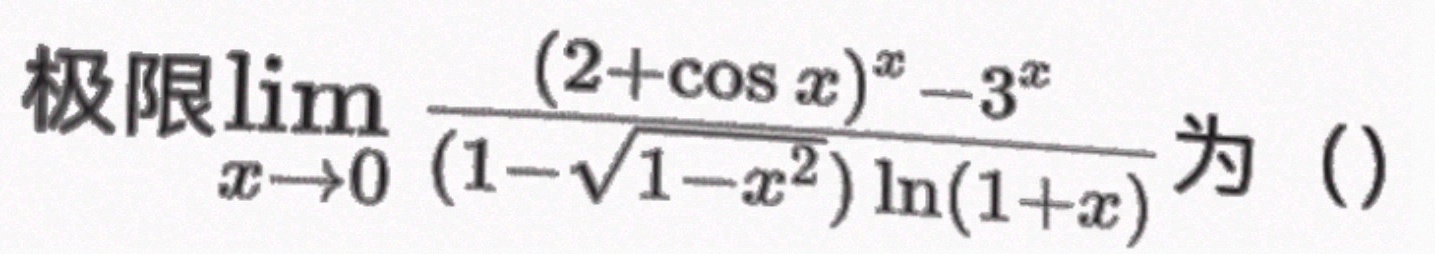
题目解答
答案

解析
步骤 1:化简分子
分子为 ${(2+\cos x)}^{x}-{3}^{x}$,当 $x\rightarrow 0$ 时,$\cos x\rightarrow 1$,因此分子可以近似为 ${(2+1)}^{x}-{3}^{x}={3}^{x}-{3}^{x}=0$。但是,我们需要更精确的近似,使用泰勒展开式。
步骤 2:泰勒展开
对于分子,使用泰勒展开式,${(2+\cos x)}^{x}$ 可以近似为 $e^{x\ln(2+\cos x)}$,而 $\ln(2+\cos x)$ 可以近似为 $\ln(3)-\dfrac{1}{6}x^2$,因此分子可以近似为 $e^{x(\ln(3)-\dfrac{1}{6}x^2)}-{3}^{x}$。
步骤 3:化简分母
分母为 $(1-\sqrt {1-{x}^{2}})\ln (1+x)$,当 $x\rightarrow 0$ 时,$\sqrt {1-{x}^{2}}\rightarrow 1$,$\ln (1+x)\rightarrow x$,因此分母可以近似为 $(1-1)\cdot x=0$。但是,我们需要更精确的近似,使用泰勒展开式。
步骤 4:泰勒展开
对于分母,使用泰勒展开式,$1-\sqrt {1-{x}^{2}}$ 可以近似为 $\dfrac{1}{2}x^2$,因此分母可以近似为 $\dfrac{1}{2}x^2\cdot x=\dfrac{1}{2}x^3$。
步骤 5:计算极限
将分子和分母的近似值代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}-{3}^{x}}{\dfrac{1}{2}x^3}$。使用洛必达法则,对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)-{3}^{x}\ln(3)}{\dfrac{3}{2}x^2}$。再次使用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)^2-{3}^{x}(\ln(3))^2}{3x}$。将 $x=0$ 代入,得到 $\dfrac {1\cdot(\ln(3))^2-1\cdot(\ln(3))^2}{0}$,即 $\dfrac {0}{0}$,再次使用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)^3-{3}^{x}(\ln(3))^3}{3}$。将 $x=0$ 代入,得到 $\dfrac {1\cdot(\ln(3))^3-1\cdot(\ln(3))^3}{3}$,即 $\dfrac {0}{3}$,即 $0$。
分子为 ${(2+\cos x)}^{x}-{3}^{x}$,当 $x\rightarrow 0$ 时,$\cos x\rightarrow 1$,因此分子可以近似为 ${(2+1)}^{x}-{3}^{x}={3}^{x}-{3}^{x}=0$。但是,我们需要更精确的近似,使用泰勒展开式。
步骤 2:泰勒展开
对于分子,使用泰勒展开式,${(2+\cos x)}^{x}$ 可以近似为 $e^{x\ln(2+\cos x)}$,而 $\ln(2+\cos x)$ 可以近似为 $\ln(3)-\dfrac{1}{6}x^2$,因此分子可以近似为 $e^{x(\ln(3)-\dfrac{1}{6}x^2)}-{3}^{x}$。
步骤 3:化简分母
分母为 $(1-\sqrt {1-{x}^{2}})\ln (1+x)$,当 $x\rightarrow 0$ 时,$\sqrt {1-{x}^{2}}\rightarrow 1$,$\ln (1+x)\rightarrow x$,因此分母可以近似为 $(1-1)\cdot x=0$。但是,我们需要更精确的近似,使用泰勒展开式。
步骤 4:泰勒展开
对于分母,使用泰勒展开式,$1-\sqrt {1-{x}^{2}}$ 可以近似为 $\dfrac{1}{2}x^2$,因此分母可以近似为 $\dfrac{1}{2}x^2\cdot x=\dfrac{1}{2}x^3$。
步骤 5:计算极限
将分子和分母的近似值代入原式,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}-{3}^{x}}{\dfrac{1}{2}x^3}$。使用洛必达法则,对分子和分母分别求导,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)-{3}^{x}\ln(3)}{\dfrac{3}{2}x^2}$。再次使用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)^2-{3}^{x}(\ln(3))^2}{3x}$。将 $x=0$ 代入,得到 $\dfrac {1\cdot(\ln(3))^2-1\cdot(\ln(3))^2}{0}$,即 $\dfrac {0}{0}$,再次使用洛必达法则,得到 $\lim _{x\rightarrow 0}\dfrac {e^{x(\ln(3)-\dfrac{1}{6}x^2)}(\ln(3)-\dfrac{1}{6}x^2)^3-{3}^{x}(\ln(3))^3}{3}$。将 $x=0$ 代入,得到 $\dfrac {1\cdot(\ln(3))^3-1\cdot(\ln(3))^3}{3}$,即 $\dfrac {0}{3}$,即 $0$。