题目
设区域 :(x)^2+(y)^2leqslant 1, 计算 =(iint )_(D)[ sin (x)^2cos (y)^2+sin (x-y)dxdy]
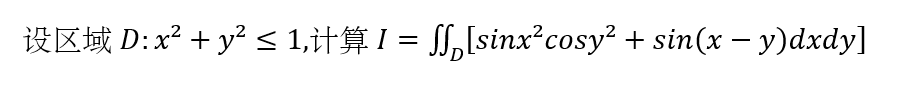
题目解答
答案

解析
考查要点:本题主要考查二重积分的对称性应用、极坐标变换以及三角函数积分的计算。
解题核心思路:
- 奇偶性简化:利用积分区域$D$的对称性,判断$\sin(x-y)$项的积分为零。
- 对称性拆分:将$\sin x^2 \cos y^2$与$\sin y^2 \cos x^2$结合,利用和角公式转化为$\sin(x^2 + y^2)$。
- 极坐标转换:将积分区域转换为极坐标,简化计算。
破题关键点:
- 奇函数在对称区域的积分性质:若被积函数为奇函数且积分区域关于原点对称,则积分为零。
- 三角恒等式:$\sin A \cos B + \cos A \sin B = \sin(A+B)$。
- 极坐标变换:将$x^2 + y^2$替换为$r^2$,雅可比行列式为$r$。
步骤1:处理$\sin(x-y)$项
由于积分区域$D$关于$x$轴和$y$轴对称,令$u = x$, $v = -y$,则$\sin(x-y)$变为$\sin(u + v)$,与原函数奇偶性相反,因此:
$\iint_D \sin(x-y) \,dx\,dy = 0$
步骤2:对称性拆分$\sin x^2 \cos y^2$
将原积分拆分为两部分并取平均:
$\iint_D \sin x^2 \cos y^2 \,dx\,dy = \frac{1}{2} \iint_D \left( \sin x^2 \cos y^2 + \sin y^2 \cos x^2 \right) \,dx\,dy$
步骤3:应用和角公式
利用$\sin A \cos B + \cos A \sin B = \sin(A+B)$,得:
$\sin x^2 \cos y^2 + \sin y^2 \cos x^2 = \sin(x^2 + y^2)$
步骤4:极坐标变换
将$x^2 + y^2 = r^2$,$dx\,dy = r \,dr\,d\theta$,积分区域变为$0 \leq r \leq 1$,$0 \leq \theta \leq 2\pi$:
$\frac{1}{2} \int_0^{2\pi} \int_0^1 r \sin r^2 \,dr\,d\theta$
步骤5:计算积分
- 对$r$积分:令$u = r^2$,则$du = 2r \,dr$,积分变为:
$\int_0^1 r \sin r^2 \,dr = \frac{1}{2} \int_0^1 \sin u \,du = \frac{1 - \cos 1}{2}$ - 对$\theta$积分:
$\int_0^{2\pi} d\theta = 2\pi$ - 合并结果:
$\frac{1}{2} \cdot 2\pi \cdot \frac{1 - \cos 1}{2} = \frac{\pi}{2}(1 - \cos 1)$