题目
(19) int dfrac (dx)(4-{x)^2}
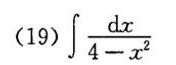
题目解答
答案
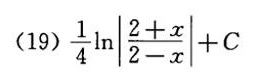
解析
考查要点:本题主要考查有理函数的积分,特别是分母为二次多项式的情况。需要掌握部分分式分解法的应用,以及对数积分的基本形式。
解题核心思路:
将分母$4 - x^2$分解为$(2 - x)(2 + x)$,利用部分分式法将其拆分为两个简单分式的和,分别积分后合并结果。关键在于正确求出部分分式的系数,并注意积分后的对数表达式形式。
破题关键点:
- 分解分母:将$4 - x^2$写成$(2 - x)(2 + x)$。
- 拆分分式:设$\dfrac{1}{4 - x^2} = \dfrac{A}{2 - x} + \dfrac{B}{2 + x}$,解出$A$和$B$。
- 分别积分:对拆分后的分式逐项积分,注意积分结果中的对数形式和绝对值符号。
步骤1:分解分母
将分母$4 - x^2$分解为两个一次因式的乘积:
$4 - x^2 = (2 - x)(2 + x).$
步骤2:部分分式分解
设$\dfrac{1}{4 - x^2} = \dfrac{A}{2 - x} + \dfrac{B}{2 + x}$,通分后得:
$1 = A(2 + x) + B(2 - x).$
步骤3:求解系数$A$和$B$
- 令$x = 2$,代入得:$1 = A(4) \Rightarrow A = \dfrac{1}{4}$。
- 令$x = -2$,代入得:$1 = B(4) \Rightarrow B = \dfrac{1}{4}$。
因此,原式可拆分为:
$\dfrac{1}{4 - x^2} = \dfrac{1}{4(2 - x)} + \dfrac{1}{4(2 + x)}.$
步骤4:逐项积分
对拆分后的分式分别积分:
- $\displaystyle \int \dfrac{1}{4(2 - x)} dx = -\dfrac{1}{4} \ln |2 - x| + C_1$(换元积分,$\int \dfrac{1}{u} du = \ln |u|$)。
- $\displaystyle \int \dfrac{1}{4(2 + x)} dx = \dfrac{1}{4} \ln |2 + x| + C_2$。
步骤5:合并结果
将两部分积分结果合并,并整理常数项:
$\dfrac{1}{4} \left( \ln |2 + x| - \ln |2 - x| \right) + C = \dfrac{1}{4} \ln \left| \dfrac{2 + x}{2 - x} \right| + C.$