题目
利用留数定理计算积分:,.
利用留数定理计算积分:,.
题目解答
答案
解:设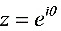 ,则
,则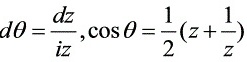 ,
,
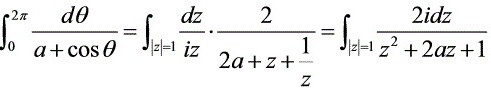
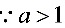 ,故奇点为
,故奇点为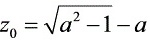
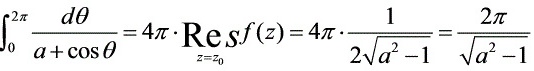 .
.
解析
步骤 1:变量替换
设 $z = e^{i\theta}$,则 $d\theta = \dfrac{dz}{iz}$,$\cos \theta = \dfrac{1}{2}(z + \dfrac{1}{z})$。这样,原积分可以转化为复平面上的积分。
步骤 2:确定奇点
由于 $a > 1$,我们需要找到函数 $\dfrac{1}{a + \cos \theta}$ 在单位圆上的奇点。将 $\cos \theta$ 用 $z$ 表示,得到 $\dfrac{1}{a + \dfrac{1}{2}(z + \dfrac{1}{z})}$。化简后,我们得到 $\dfrac{2z}{2az + z^2 + 1}$。令分母为零,解得 $z^2 + 2az + 1 = 0$,解得 $z = -a \pm \sqrt{a^2 - 1}$。由于 $a > 1$,只有 $z = -a + \sqrt{a^2 - 1}$ 在单位圆内,即为奇点。
步骤 3:计算留数
计算在 $z = -a + \sqrt{a^2 - 1}$ 处的留数。留数为 $\lim_{z \to -a + \sqrt{a^2 - 1}} \dfrac{2z}{2a + z + \dfrac{1}{z}}$。将 $z = -a + \sqrt{a^2 - 1}$ 代入,得到留数为 $\dfrac{1}{\sqrt{a^2 - 1}}$。
步骤 4:应用留数定理
根据留数定理,积分值等于 $2\pi i$ 乘以留数。因此,积分值为 $2\pi i \cdot \dfrac{1}{\sqrt{a^2 - 1}}$。由于积分是实数,我们只取实部,即 $\dfrac{2\pi}{\sqrt{a^2 - 1}}$。
设 $z = e^{i\theta}$,则 $d\theta = \dfrac{dz}{iz}$,$\cos \theta = \dfrac{1}{2}(z + \dfrac{1}{z})$。这样,原积分可以转化为复平面上的积分。
步骤 2:确定奇点
由于 $a > 1$,我们需要找到函数 $\dfrac{1}{a + \cos \theta}$ 在单位圆上的奇点。将 $\cos \theta$ 用 $z$ 表示,得到 $\dfrac{1}{a + \dfrac{1}{2}(z + \dfrac{1}{z})}$。化简后,我们得到 $\dfrac{2z}{2az + z^2 + 1}$。令分母为零,解得 $z^2 + 2az + 1 = 0$,解得 $z = -a \pm \sqrt{a^2 - 1}$。由于 $a > 1$,只有 $z = -a + \sqrt{a^2 - 1}$ 在单位圆内,即为奇点。
步骤 3:计算留数
计算在 $z = -a + \sqrt{a^2 - 1}$ 处的留数。留数为 $\lim_{z \to -a + \sqrt{a^2 - 1}} \dfrac{2z}{2a + z + \dfrac{1}{z}}$。将 $z = -a + \sqrt{a^2 - 1}$ 代入,得到留数为 $\dfrac{1}{\sqrt{a^2 - 1}}$。
步骤 4:应用留数定理
根据留数定理,积分值等于 $2\pi i$ 乘以留数。因此,积分值为 $2\pi i \cdot \dfrac{1}{\sqrt{a^2 - 1}}$。由于积分是实数,我们只取实部,即 $\dfrac{2\pi}{\sqrt{a^2 - 1}}$。