题目
[例5] 设函数f(x,y)连续,则 (int )_(1)^2dx(int )_(x)^2f(x,y)dy+(int )_(1)^2dy(int )_(y)^4-yf(x,y)dx 等于 ()-|||-(A) (int )_(1)^2dx(int )_(1)^4-xf(x,y)dy (B) (int )_(1)^2dx(int )_(x)^4-xf(x,y)dy-|||-(C) (int )_(1)^2dy(int )_(1)^4-yf(x,y)dx (D) (int )_(1)^2dy(int )_(y)^2f(x,y)dx
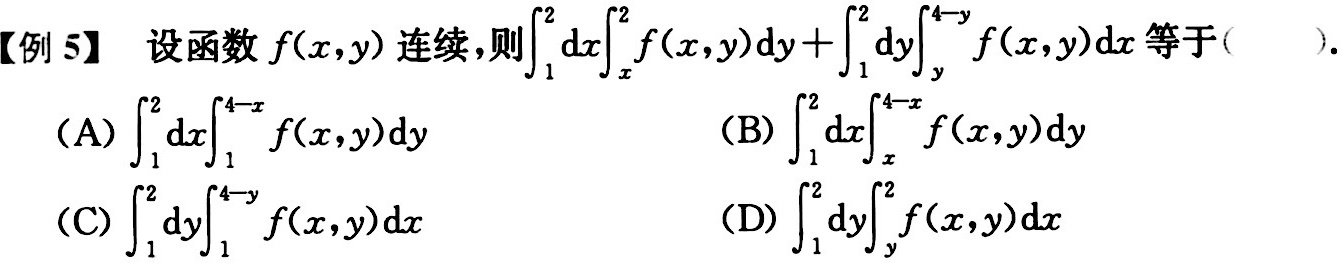
题目解答
答案
解析
步骤 1：确定积分区域
首先，我们确定两个积分的积分区域。第一个积分 ${\int }_{1}^{2}dx{\int }_{x}^{2}f(x,y)dy$ 的积分区域为 ${D}_{1}=\{ (x,y)|1\leqslant x\leqslant 2,x\leqslant y\leqslant 2\}$。第二个积分 ${\int }_{1}^{2}dy{\int }_{y}^{4-y}f(x,y)dx$ 的积分区域为 ${D}_{2}=\{ (x,y)|1\leqslant y\leqslant 2,y\leqslant x\leqslant 4-y\}$。
步骤 2：合并积分区域
将两个积分区域合并，得到 $D=\{ (x,y)|1\leqslant y\leqslant 2,1\leqslant x\leqslant 4-y\}$。
步骤 3：交换积分次序
将合并后的积分区域 $D$ 用于交换积分次序，得到 ${\int }_{1}^{2}dy{\int }_{1}^{4-y}f(x,y)dx$。
首先，我们确定两个积分的积分区域。第一个积分 ${\int }_{1}^{2}dx{\int }_{x}^{2}f(x,y)dy$ 的积分区域为 ${D}_{1}=\{ (x,y)|1\leqslant x\leqslant 2,x\leqslant y\leqslant 2\}$。第二个积分 ${\int }_{1}^{2}dy{\int }_{y}^{4-y}f(x,y)dx$ 的积分区域为 ${D}_{2}=\{ (x,y)|1\leqslant y\leqslant 2,y\leqslant x\leqslant 4-y\}$。
步骤 2：合并积分区域
将两个积分区域合并，得到 $D=\{ (x,y)|1\leqslant y\leqslant 2,1\leqslant x\leqslant 4-y\}$。
步骤 3：交换积分次序
将合并后的积分区域 $D$ 用于交换积分次序，得到 ${\int }_{1}^{2}dy{\int }_{1}^{4-y}f(x,y)dx$。