题目
若f(x)的定义域为[-1,2]，则F(x)=f(2x)+f(2+x)的定义域为
若f(x)的定义域为[-1,2]，则F(x)=f(2x)+f(2+x)的定义域为
题目解答
答案
解：
根据题意，由于f(x)的定义域为[-1,2]，
则对于函数F(x)=f(2x)+f(2+x)
可得-1≤2x≤2并且-1≤2+x≤2
对于第一个不等式，得到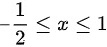
对于第二个不等式，得到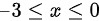
则取两个不等式的解的交集
得到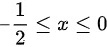
综上所述：该函数的定义域为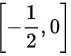
解析
步骤 1：确定f(2x)的定义域
由于f(x)的定义域为[-1,2]，则对于f(2x)，需要满足-1≤2x≤2。解这个不等式得到$-\dfrac {1}{2}\leqslant x\leqslant 1$。
步骤 2：确定f(2+x)的定义域
同样地，对于f(2+x)，需要满足-1≤2+x≤2。解这个不等式得到-3≤x≤0。
步骤 3：求两个定义域的交集
由于F(x)=f(2x)+f(2+x)，则x需要同时满足两个条件，即$-\dfrac {1}{2}\leqslant x\leqslant 1$和-3≤x≤0。因此，x的取值范围是这两个不等式的交集，即$-\dfrac {1}{2}\leqslant x\leqslant 0$。
由于f(x)的定义域为[-1,2]，则对于f(2x)，需要满足-1≤2x≤2。解这个不等式得到$-\dfrac {1}{2}\leqslant x\leqslant 1$。
步骤 2：确定f(2+x)的定义域
同样地，对于f(2+x)，需要满足-1≤2+x≤2。解这个不等式得到-3≤x≤0。
步骤 3：求两个定义域的交集
由于F(x)=f(2x)+f(2+x)，则x需要同时满足两个条件，即$-\dfrac {1}{2}\leqslant x\leqslant 1$和-3≤x≤0。因此，x的取值范围是这两个不等式的交集，即$-\dfrac {1}{2}\leqslant x\leqslant 0$。