题目
(2)设函数f(x)在[0,1]上二阶可导,且 (int )_(0)^1f(x)dx=0, 则-|||-(A)当 '(x)lt 0 时, (dfrac (1)(2))lt 0. (B)当 ''(x)lt 0 时, (dfrac (1)(2))lt 0.-|||-(C)当 '(x)gt 0 时, (dfrac (1)(2))lt 0. (D)当 ''(x)gt 0 时, (dfrac (1)(2))lt 0.A、AB、BC、CD、D
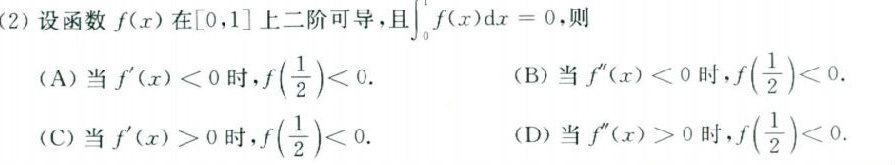
- A、A
- B、B
- C、C
- D、D
题目解答
答案
D
解析
步骤 1：理解条件
函数 $f(x)$ 在区间 $[0,1]$ 上二阶可导，且 $\int_0^1 f(x)dx = 0$。这意味着函数 $f(x)$ 在区间 $[0,1]$ 上的积分值为零。
步骤 2：分析选项
(A) 当 $f'(x) < 0$ 时，$f(\frac{1}{2}) < 0$。
(B) 当 $f'(x) < 0$ 时，$f(\frac{1}{2}) < 0$。
(C) 当 $f'(x) > 0$ 时，$f(\frac{1}{2}) < 0$。
(D) 当 $f''(x) > 0$ 时，$f(\frac{1}{2}) < 0$。
步骤 3：分析函数性质
由于 $f(x)$ 在 $[0,1]$ 上二阶可导，且 $\int_0^1 f(x)dx = 0$，说明 $f(x)$ 在 $[0,1]$ 上的平均值为零。如果 $f''(x) > 0$，则 $f(x)$ 在 $[0,1]$ 上是凹函数，即 $f(x)$ 在 $[0,1]$ 上的图形是向下凹的。由于 $f(x)$ 在 $[0,1]$ 上的平均值为零，且 $f(x)$ 是凹函数，因此 $f(\frac{1}{2})$ 必须小于零。
函数 $f(x)$ 在区间 $[0,1]$ 上二阶可导，且 $\int_0^1 f(x)dx = 0$。这意味着函数 $f(x)$ 在区间 $[0,1]$ 上的积分值为零。
步骤 2：分析选项
(A) 当 $f'(x) < 0$ 时，$f(\frac{1}{2}) < 0$。
(B) 当 $f'(x) < 0$ 时，$f(\frac{1}{2}) < 0$。
(C) 当 $f'(x) > 0$ 时，$f(\frac{1}{2}) < 0$。
(D) 当 $f''(x) > 0$ 时，$f(\frac{1}{2}) < 0$。
步骤 3：分析函数性质
由于 $f(x)$ 在 $[0,1]$ 上二阶可导，且 $\int_0^1 f(x)dx = 0$，说明 $f(x)$ 在 $[0,1]$ 上的平均值为零。如果 $f''(x) > 0$，则 $f(x)$ 在 $[0,1]$ 上是凹函数，即 $f(x)$ 在 $[0,1]$ 上的图形是向下凹的。由于 $f(x)$ 在 $[0,1]$ 上的平均值为零，且 $f(x)$ 是凹函数，因此 $f(\frac{1}{2})$ 必须小于零。