题目
13、求一阶线性微分方程-2xy=4x(e)^(x^2)的通解。
13、求一阶线性微分方程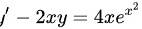 的通解。
的通解。
题目解答
答案
由题可得:
该一阶线性微分方程为: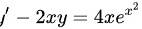
代入一阶线性微分方程的通解公式可得:
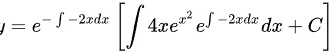
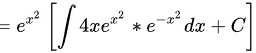
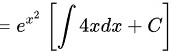
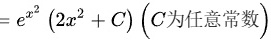
所以该方程的通解为:
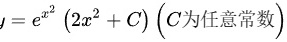
解析
步骤 1:确定微分方程的形式
给定的微分方程为$-2xy=4x{e}^{{x}^{2}}$,可以重写为$y'+2xy=4{e}^{{x}^{2}}$,其中$y'$表示$y$对$x$的导数。这是一个一阶线性微分方程,形式为$y'+P(x)y=Q(x)$,其中$P(x)=2x$,$Q(x)=4{e}^{{x}^{2}}$。
步骤 2:求解积分因子
一阶线性微分方程的通解公式为$y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$。首先,计算积分因子$e^{-\int P(x)dx}$,即$e^{-\int 2xdx}=e^{-x^2}$。
步骤 3:计算通解
将$Q(x)$和积分因子代入通解公式,得到$y=e^{-x^2}[\int 4{e}^{{x}^{2}}e^{x^2}dx+C]=e^{-x^2}[\int 4dx+C]=e^{-x^2}[4x+C]$。因此,该方程的通解为$y=e^{-x^2}(4x+C)$,其中$C$为任意常数。
给定的微分方程为$-2xy=4x{e}^{{x}^{2}}$,可以重写为$y'+2xy=4{e}^{{x}^{2}}$,其中$y'$表示$y$对$x$的导数。这是一个一阶线性微分方程,形式为$y'+P(x)y=Q(x)$,其中$P(x)=2x$,$Q(x)=4{e}^{{x}^{2}}$。
步骤 2:求解积分因子
一阶线性微分方程的通解公式为$y=e^{-\int P(x)dx}[\int Q(x)e^{\int P(x)dx}dx+C]$。首先,计算积分因子$e^{-\int P(x)dx}$,即$e^{-\int 2xdx}=e^{-x^2}$。
步骤 3:计算通解
将$Q(x)$和积分因子代入通解公式,得到$y=e^{-x^2}[\int 4{e}^{{x}^{2}}e^{x^2}dx+C]=e^{-x^2}[\int 4dx+C]=e^{-x^2}[4x+C]$。因此,该方程的通解为$y=e^{-x^2}(4x+C)$,其中$C$为任意常数。