题目
求不定积分int dfrac (2{x)^2cos 4x-3}({x)^2}dx
求不定积分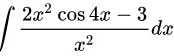
题目解答
答案
根据不定积分的性质直接计算即可:
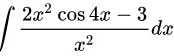
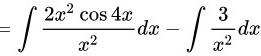
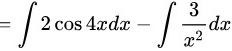
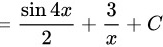
解析
考查要点:本题主要考查不定积分的基本性质和积分技巧,特别是分式拆分与分项积分的能力,以及对基本积分公式的熟练应用。
解题核心思路:
- 分式拆分:将被积函数的分子拆分为两个部分,分别除以分母,从而将原积分转化为两个更简单的积分之和。
- 逐项积分:分别对拆分后的两个积分应用基本积分公式,其中涉及三角函数积分和幂函数积分。
- 合并结果:将两个积分的结果相加,并添加积分常数。
破题关键点:
- 正确拆分分子:通过分子分母约简简化被积函数。
- 熟练应用积分公式:如$\int \cos(ax) dx = \frac{\sin(ax)}{a} + C$和$\int x^n dx = \frac{x^{n+1}}{n+1} + C$($n \neq -1$)。
步骤1:拆分被积函数
将原积分拆分为两个积分之差:
$\int \frac{2x^2 \cos 4x - 3}{x^2} dx = \int \frac{2x^2 \cos 4x}{x^2} dx - \int \frac{3}{x^2} dx.$
步骤2:简化被积函数
约简分式中的$x^2$:
$\int 2 \cos 4x \, dx - \int \frac{3}{x^2} dx.$
步骤3:逐项积分
-
第一项积分:
应用三角函数积分公式$\int \cos(ax) dx = \frac{\sin(ax)}{a} + C$:
$\int 2 \cos 4x \, dx = 2 \cdot \frac{\sin 4x}{4} = \frac{\sin 4x}{2}.$ -
第二项积分:
将$\frac{3}{x^2}$写成$3x^{-2}$,应用幂函数积分公式$\int x^n dx = \frac{x^{n+1}}{n+1} + C$($n \neq -1$):
$\int \frac{3}{x^2} dx = 3 \int x^{-2} dx = 3 \cdot \frac{x^{-1}}{-1} = -\frac{3}{x}.$
步骤4:合并结果
将两部分积分结果相加,并添加积分常数$C$:
$\frac{\sin 4x}{2} + \frac{3}{x} + C.$