题目
求函数 (x)=(x)^2ln (1+x) 在 x=0 处的n阶导数 '(n)(0)(ngeqslant 3
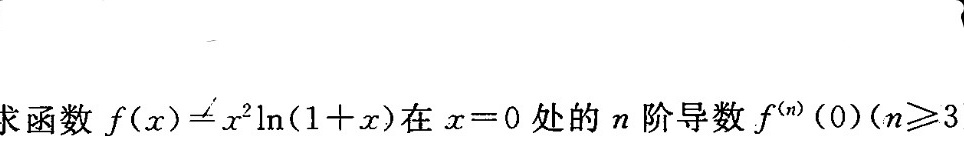
题目解答
答案
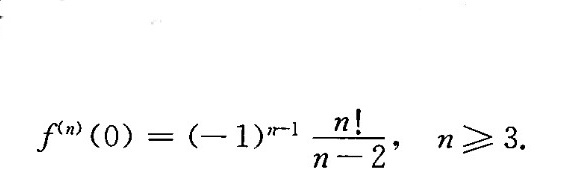
解析
考查要点:本题主要考查函数在某点的高阶导数求解,特别是利用泰勒展开(麦克劳林级数)的方法简化高阶导数的计算。
解题核心思路:
- 将函数分解为已知泰勒展开式的乘积:将$f(x) = x^2 \ln(1+x)$拆分为$x^2$与$\ln(1+x)$的乘积。
- 展开$\ln(1+x)$的麦克劳林级数:利用已知的$\ln(1+x)$的展开式,将其与$x^2$相乘,得到$f(x)$的幂级数表达式。
- 提取$x^n$项的系数:通过级数中$x^n$项的系数与高阶导数的关系,直接求出$f^{(n)}(0)$。
破题关键点:
- 避免直接求高阶导数:直接求高阶导数会因复杂度高而难以处理,转而通过级数展开更高效。
- 正确处理级数的起始项:注意$\ln(1+x)$展开后从$x^1$开始,与$x^2$相乘后起始项为$x^3$,需对应$n \geq 3$的条件。
-
展开$\ln(1+x)$的麦克劳林级数
$\ln(1+x)$的展开式为:
$\ln(1+x) = \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} x^k \quad (|x| < 1)$ -
与$x^2$相乘得到$f(x)$的级数
将$x^2$乘以$\ln(1+x)$的展开式:
$f(x) = x^2 \cdot \ln(1+x) = x^2 \cdot \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} x^k = \sum_{k=1}^{\infty} \frac{(-1)^{k+1}}{k} x^{k+2}$ -
调整求和指标
令$m = k + 2$,则$k = m - 2$,当$k \geq 1$时,$m \geq 3$。级数变为:
$f(x) = \sum_{m=3}^{\infty} \frac{(-1)^{(m-2)+1}}{m-2} x^m = \sum_{m=3}^{\infty} \frac{(-1)^{m-1}}{m-2} x^m$ -
提取$x^n$项的系数
当$n \geq 3$时,$x^n$项的系数为$\frac{(-1)^{n-1}}{n-2}$。根据麦克劳林级数的通项公式:
$\frac{f^{(n)}(0)}{n!} = \frac{(-1)^{n-1}}{n-2}$
解得:
$f^{(n)}(0) = (-1)^{n-1} \cdot \frac{n!}{n-2}$