题目
若varepsilon sim B(4,dfrac (1)(2)),则由切比雪夫不等式估计varepsilon sim B(4,dfrac (1)(2))
若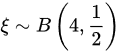
,则由切比雪夫不等式估计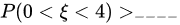
题目解答
答案
因为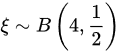
所以有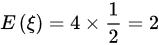
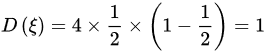
由切比雪夫不等式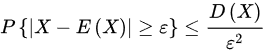
代入可得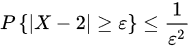
若求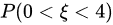
取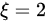
即可得
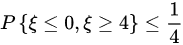
所以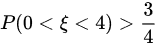
解析
步骤 1：确定随机变量的期望和方差
由于$\varepsilon \sim B(4,\dfrac {1}{2})$，这是一个二项分布，其中$n=4$，$p=\dfrac {1}{2}$。对于二项分布，期望$E(\xi )=np$，方差$D(\xi )=np(1-p)$。因此，$E(\xi )=4\times \dfrac {1}{2}=2$，$D(\xi )=4\times \dfrac {1}{2}\times (1-\dfrac {1}{2})=1$。
步骤 2：应用切比雪夫不等式
切比雪夫不等式表明，对于任意随机变量$X$，有$P\{ |X-E(X)|\geqslant e\} \leqslant \dfrac {D(X)}{{e}^{2}}$。将$E(\xi )=2$和$D(\xi )=1$代入，得到$P\{ |\xi -2|\geqslant e\} \leqslant \dfrac {1}{{e}^{2}}$。
步骤 3：计算$P(0\lt \xi \lt 4)$
为了计算$P(0\lt \xi \lt 4)$，我们需要计算$P\{ \xi \leqslant 0,\xi \geqslant 4\}$。根据切比雪夫不等式，取$e=2$，得到$P\{ |\xi -2|\geqslant 2\} \leqslant \dfrac {1}{4}$。因此，$P\{ \xi \leqslant 0,\xi \geqslant 4\} \leqslant \dfrac {1}{4}$。所以$P(0\lt \xi \lt 4)=1-P\{ \xi \leqslant 0,\xi \geqslant 4\} \gt 1-\dfrac {1}{4}=\dfrac {3}{4}$。
由于$\varepsilon \sim B(4,\dfrac {1}{2})$，这是一个二项分布，其中$n=4$，$p=\dfrac {1}{2}$。对于二项分布，期望$E(\xi )=np$，方差$D(\xi )=np(1-p)$。因此，$E(\xi )=4\times \dfrac {1}{2}=2$，$D(\xi )=4\times \dfrac {1}{2}\times (1-\dfrac {1}{2})=1$。
步骤 2：应用切比雪夫不等式
切比雪夫不等式表明，对于任意随机变量$X$，有$P\{ |X-E(X)|\geqslant e\} \leqslant \dfrac {D(X)}{{e}^{2}}$。将$E(\xi )=2$和$D(\xi )=1$代入，得到$P\{ |\xi -2|\geqslant e\} \leqslant \dfrac {1}{{e}^{2}}$。
步骤 3：计算$P(0\lt \xi \lt 4)$
为了计算$P(0\lt \xi \lt 4)$，我们需要计算$P\{ \xi \leqslant 0,\xi \geqslant 4\}$。根据切比雪夫不等式，取$e=2$，得到$P\{ |\xi -2|\geqslant 2\} \leqslant \dfrac {1}{4}$。因此，$P\{ \xi \leqslant 0,\xi \geqslant 4\} \leqslant \dfrac {1}{4}$。所以$P(0\lt \xi \lt 4)=1-P\{ \xi \leqslant 0,\xi \geqslant 4\} \gt 1-\dfrac {1}{4}=\dfrac {3}{4}$。