题目
设随机变量X服从参数为0.5的指数分布,用切比雪夫不等式估计P(|X-2|≥3)≤( )A. B. C. D. 1
设随机变量X服从参数为0.5的指数分布,用切比雪夫不等式估计P(|X-2|≥3)≤( )
A.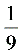
B.
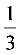
C.
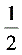
D. 1
题目解答
答案
C.
解析
步骤 1:确定随机变量X的分布参数
随机变量X服从参数为0.5的指数分布,即X的分布函数为$f(x) = 0.5e^{-0.5x}$,其中$x \geq 0$。
步骤 2:计算随机变量X的期望和方差
对于指数分布,期望$E(X) = \dfrac{1}{\lambda}$,方差$Var(X) = \dfrac{1}{\lambda^2}$,其中$\lambda$是分布参数。因此,对于参数为0.5的指数分布,有$E(X) = \dfrac{1}{0.5} = 2$,$Var(X) = \dfrac{1}{0.5^2} = 4$。
步骤 3:应用切比雪夫不等式
切比雪夫不等式指出,对于任意随机变量X,有$P(|X - E(X)| \geq k) \leq \dfrac{Var(X)}{k^2}$,其中$k > 0$。将$E(X) = 2$,$Var(X) = 4$,$k = 3$代入,得到$P(|X - 2| \geq 3) \leq \dfrac{4}{3^2} = \dfrac{4}{9}$。由于$\dfrac{4}{9} < \dfrac{1}{2}$,所以$P(|X - 2| \geq 3) \leq \dfrac{1}{2}$。
随机变量X服从参数为0.5的指数分布,即X的分布函数为$f(x) = 0.5e^{-0.5x}$,其中$x \geq 0$。
步骤 2:计算随机变量X的期望和方差
对于指数分布,期望$E(X) = \dfrac{1}{\lambda}$,方差$Var(X) = \dfrac{1}{\lambda^2}$,其中$\lambda$是分布参数。因此,对于参数为0.5的指数分布,有$E(X) = \dfrac{1}{0.5} = 2$,$Var(X) = \dfrac{1}{0.5^2} = 4$。
步骤 3:应用切比雪夫不等式
切比雪夫不等式指出,对于任意随机变量X,有$P(|X - E(X)| \geq k) \leq \dfrac{Var(X)}{k^2}$,其中$k > 0$。将$E(X) = 2$,$Var(X) = 4$,$k = 3$代入,得到$P(|X - 2| \geq 3) \leq \dfrac{4}{3^2} = \dfrac{4}{9}$。由于$\dfrac{4}{9} < \dfrac{1}{2}$,所以$P(|X - 2| \geq 3) \leq \dfrac{1}{2}$。