题目
调整某种仪器 100 台 ,设调整无误的概率为 0 ,调整过大成过小的概率都是dfrac (1)(2),用切比雪夫不等式估计调整过大的仪器数在 40 台 到 60 台 之间的概率范围是 A . 大于等于dfrac (1)(2)B. 小于等于dfrac (1)(2)C. 小于等于dfrac (1)(2)D. 大于等于dfrac (1)(2)
调整某种仪器 100 台 ,设调整无误的概率为 0 ,调整过大成过小的概率都是 ,用切比雪夫不等式估计调整过大的仪器数在 40 台 到 60 台 之间的概率范围是
,用切比雪夫不等式估计调整过大的仪器数在 40 台 到 60 台 之间的概率范围是
A . 大于等于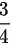
B. 小于等于
C. 小于等于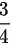
D. 大于等于
题目解答
答案
已知调整某种仪器 100 台 ,调整过大成过小的概率都是 ,则调整过大的仪器数X服从二项分布
,则调整过大的仪器数X服从二项分布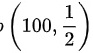 ,则
,则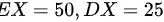 .
.
则根据切比雪夫不等式,可得调整过大的仪器数在 40 台 到 60 台 之间的概率范围为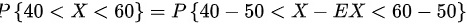
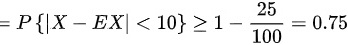
本题选A.
解析
步骤 1:确定随机变量的分布
调整某种仪器 100 台,调整过大成过小的概率都是$\dfrac {1}{2}$,则调整过大的仪器数X服从二项分布$(100,\dfrac {1}{2})$。
步骤 2:计算期望和方差
对于二项分布$(n,p)$,期望$E(X)=np$,方差$D(X)=np(1-p)$。因此,$E(X)=100\times\dfrac{1}{2}=50$,$D(X)=100\times\dfrac{1}{2}\times\dfrac{1}{2}=25$。
步骤 3:应用切比雪夫不等式
切比雪夫不等式指出,对于任意随机变量$X$,其期望为$E(X)$,方差为$D(X)$,对于任意正数$\varepsilon$,有$P(|X-E(X)|\geqslant \varepsilon)\leqslant \dfrac{D(X)}{\varepsilon^2}$。因此,调整过大的仪器数在 40 台 到 60 台 之间的概率范围为$P(40
调整某种仪器 100 台,调整过大成过小的概率都是$\dfrac {1}{2}$,则调整过大的仪器数X服从二项分布$(100,\dfrac {1}{2})$。
步骤 2:计算期望和方差
对于二项分布$(n,p)$,期望$E(X)=np$,方差$D(X)=np(1-p)$。因此,$E(X)=100\times\dfrac{1}{2}=50$,$D(X)=100\times\dfrac{1}{2}\times\dfrac{1}{2}=25$。
步骤 3:应用切比雪夫不等式
切比雪夫不等式指出,对于任意随机变量$X$,其期望为$E(X)$,方差为$D(X)$,对于任意正数$\varepsilon$,有$P(|X-E(X)|\geqslant \varepsilon)\leqslant \dfrac{D(X)}{\varepsilon^2}$。因此,调整过大的仪器数在 40 台 到 60 台 之间的概率范围为$P(40