题目
[单选题] 函数 f(x)= { ,xneq 0 1, x=0 . '在 x=0 处A.连续且取得极大值B.连续且取得极小值C.可导且导数为零D.可导且导数不为零
[单选题] 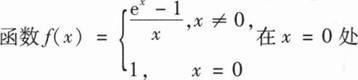
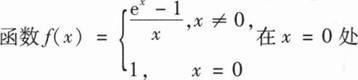
- A.连续且取得极大值
- B.连续且取得极小值
- C.可导且导数为零
- D.可导且导数不为零
题目解答
答案
D. 可导且导数不为零
解析
步骤 1:判断函数在 x=0 处的连续性
函数在 x=0 处的定义为 f(0)=1,而当 x≠0 时,函数为 $\dfrac {{e}^{x}-1}{x}$。为了判断函数在 x=0 处的连续性,我们需要计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x}$。
步骤 2:计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x}$
根据洛必达法则,$\lim_{x \to 0} \dfrac {{e}^{x}-1}{x} = \lim_{x \to 0} \dfrac {{e}^{x}}{1} = 1$。因此,函数在 x=0 处连续。
步骤 3:判断函数在 x=0 处的可导性
为了判断函数在 x=0 处的可导性,我们需要计算 $\lim_{x \to 0} \dfrac {f(x)-f(0)}{x-0}$。根据步骤 1 和步骤 2,我们已经知道 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x} = 1$,因此 $\lim_{x \to 0} \dfrac {f(x)-f(0)}{x-0} = \lim_{x \to 0} \dfrac {\dfrac {{e}^{x}-1}{x}-1}{x} = \lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2}$。
步骤 4:计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2}$
根据洛必达法则,$\lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2} = \lim_{x \to 0} \dfrac {{e}^{x}-1}{2x} = \lim_{x \to 0} \dfrac {{e}^{x}}{2} = \dfrac {1}{2}$。因此,函数在 x=0 处可导且导数不为零。
函数在 x=0 处的定义为 f(0)=1,而当 x≠0 时,函数为 $\dfrac {{e}^{x}-1}{x}$。为了判断函数在 x=0 处的连续性,我们需要计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x}$。
步骤 2:计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x}$
根据洛必达法则,$\lim_{x \to 0} \dfrac {{e}^{x}-1}{x} = \lim_{x \to 0} \dfrac {{e}^{x}}{1} = 1$。因此,函数在 x=0 处连续。
步骤 3:判断函数在 x=0 处的可导性
为了判断函数在 x=0 处的可导性,我们需要计算 $\lim_{x \to 0} \dfrac {f(x)-f(0)}{x-0}$。根据步骤 1 和步骤 2,我们已经知道 $\lim_{x \to 0} \dfrac {{e}^{x}-1}{x} = 1$,因此 $\lim_{x \to 0} \dfrac {f(x)-f(0)}{x-0} = \lim_{x \to 0} \dfrac {\dfrac {{e}^{x}-1}{x}-1}{x} = \lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2}$。
步骤 4:计算 $\lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2}$
根据洛必达法则,$\lim_{x \to 0} \dfrac {{e}^{x}-1-x}{x^2} = \lim_{x \to 0} \dfrac {{e}^{x}-1}{2x} = \lim_{x \to 0} \dfrac {{e}^{x}}{2} = \dfrac {1}{2}$。因此,函数在 x=0 处可导且导数不为零。