题目
函数(x)=|x-(x)^2|((e)^x-1)+sin |x-2|不可导点的个数为（ ）(x)=|x-(x)^2|((e)^x-1)+sin |x-2|(x)=|x-(x)^2|((e)^x-1)+sin |x-2|(x)=|x-(x)^2|((e)^x-1)+sin |x-2|(x)=|x-(x)^2|((e)^x-1)+sin |x-2|
函数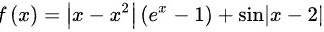
不可导点的个数为（ ）
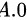
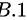
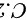
题目解答
答案
对于函数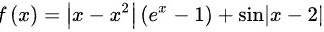
可知其不存在的点或函数分段的点为
,
,
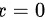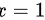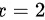
当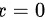时
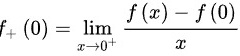
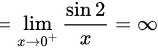
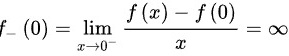
左右导数不存在，所以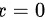处不可导。
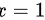当时。
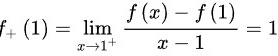
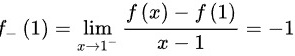
左右导数不相等，故当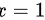时不可导。
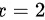当时。
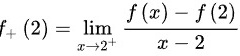
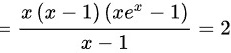
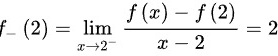
左右导数相等，故当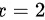时函数可导。
所以函数在
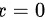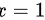,时不可导。有两个不可导点。
所以本题答案选C.
解析
步骤 1：确定函数的分段点
函数$f(x)=|x-{x}^{2}|({e}^{x}-1)+\sin |x-2|$中，绝对值函数$|x-{x}^{2}|$和$|x-2|$的分段点分别为$x=0$，$x=1$和$x=2$。这些点可能是函数不可导的点。
步骤 2：检查$x=0$处的可导性
在$x=0$处，函数$f(x)$的表达式为$f(x)=x(1-x)({e}^{x}-1)+\sin |x-2|$。由于$|x-2|$在$x=0$处连续，我们主要关注$|x-{x}^{2}|({e}^{x}-1)$在$x=0$处的可导性。由于$|x-{x}^{2}|$在$x=0$处不可导，因此$f(x)$在$x=0$处不可导。
步骤 3：检查$x=1$处的可导性
在$x=1$处，函数$f(x)$的表达式为$f(x)=(1-x)(x-1)({e}^{x}-1)+\sin |x-2|$。由于$|x-{x}^{2}|$在$x=1$处不可导，因此$f(x)$在$x=1$处不可导。
步骤 4：检查$x=2$处的可导性
在$x=2$处，函数$f(x)$的表达式为$f(x)=|x-{x}^{2}|({e}^{x}-1)+\sin (x-2)$。由于$|x-{x}^{2}|$在$x=2$处连续且可导，因此$f(x)$在$x=2$处可导。
函数$f(x)=|x-{x}^{2}|({e}^{x}-1)+\sin |x-2|$中，绝对值函数$|x-{x}^{2}|$和$|x-2|$的分段点分别为$x=0$，$x=1$和$x=2$。这些点可能是函数不可导的点。
步骤 2：检查$x=0$处的可导性
在$x=0$处，函数$f(x)$的表达式为$f(x)=x(1-x)({e}^{x}-1)+\sin |x-2|$。由于$|x-2|$在$x=0$处连续，我们主要关注$|x-{x}^{2}|({e}^{x}-1)$在$x=0$处的可导性。由于$|x-{x}^{2}|$在$x=0$处不可导，因此$f(x)$在$x=0$处不可导。
步骤 3：检查$x=1$处的可导性
在$x=1$处，函数$f(x)$的表达式为$f(x)=(1-x)(x-1)({e}^{x}-1)+\sin |x-2|$。由于$|x-{x}^{2}|$在$x=1$处不可导，因此$f(x)$在$x=1$处不可导。
步骤 4：检查$x=2$处的可导性
在$x=2$处，函数$f(x)$的表达式为$f(x)=|x-{x}^{2}|({e}^{x}-1)+\sin (x-2)$。由于$|x-{x}^{2}|$在$x=2$处连续且可导，因此$f(x)$在$x=2$处可导。