题目
已知Σ为锥面=sqrt ({x)^2+(y)^2}在柱体=sqrt ({x)^2+(y)^2}内的部分,则曲面积分=sqrt ({x)^2+(y)^2} (A)=sqrt ({x)^2+(y)^2} (B)=sqrt ({x)^2+(y)^2} (C)2 (D)0
已知Σ为锥面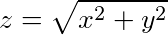
在柱体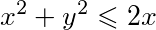
内的部分,则曲面积分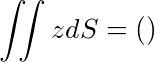
(A)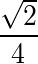
(B)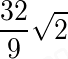
(C)2
(D)0
题目解答
答案
(B)
解析
步骤 1：确定积分区域
锥面$z=\sqrt{x^{2}+y^{2}}$在柱体$x^{2}+y^{2}\leqslant 2x$内的部分，可以转换为极坐标形式，即$r^2 \leq 2r\cos\theta$，从而得到$r \leq 2\cos\theta$。积分区域为$0 \leq \theta \leq \frac{\pi}{2}$，$0 \leq r \leq 2\cos\theta$。
步骤 2：计算曲面元素$dS$
曲面$z=\sqrt{x^{2}+y^{2}}$的曲面元素$dS$可以表示为$\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}dxdy$。由于$z=\sqrt{x^{2}+y^{2}}$，则$\frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}}}$，$\frac{\partial z}{\partial y}=\frac{y}{\sqrt{x^{2}+y^{2}}}$，从而$dS=\sqrt{2}dxdy$。
步骤 3：计算曲面积分
将$dS$和$z$代入曲面积分$\iint zdS$，得到$\iint \sqrt{x^{2}+y^{2}}\sqrt{2}dxdy$。转换为极坐标形式，得到$\iint \sqrt{r^2}\sqrt{2}rdrd\theta$。积分区域为$0 \leq \theta \leq \frac{\pi}{2}$，$0 \leq r \leq 2\cos\theta$，从而得到$\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos\theta}r^2\sqrt{2}drd\theta$。计算得到$\frac{32}{9}\sqrt{2}$。
锥面$z=\sqrt{x^{2}+y^{2}}$在柱体$x^{2}+y^{2}\leqslant 2x$内的部分，可以转换为极坐标形式，即$r^2 \leq 2r\cos\theta$，从而得到$r \leq 2\cos\theta$。积分区域为$0 \leq \theta \leq \frac{\pi}{2}$，$0 \leq r \leq 2\cos\theta$。
步骤 2：计算曲面元素$dS$
曲面$z=\sqrt{x^{2}+y^{2}}$的曲面元素$dS$可以表示为$\sqrt{1+(\frac{\partial z}{\partial x})^2+(\frac{\partial z}{\partial y})^2}dxdy$。由于$z=\sqrt{x^{2}+y^{2}}$，则$\frac{\partial z}{\partial x}=\frac{x}{\sqrt{x^{2}+y^{2}}}$，$\frac{\partial z}{\partial y}=\frac{y}{\sqrt{x^{2}+y^{2}}}$，从而$dS=\sqrt{2}dxdy$。
步骤 3：计算曲面积分
将$dS$和$z$代入曲面积分$\iint zdS$，得到$\iint \sqrt{x^{2}+y^{2}}\sqrt{2}dxdy$。转换为极坐标形式，得到$\iint \sqrt{r^2}\sqrt{2}rdrd\theta$。积分区域为$0 \leq \theta \leq \frac{\pi}{2}$，$0 \leq r \leq 2\cos\theta$，从而得到$\int_{0}^{\frac{\pi}{2}}\int_{0}^{2\cos\theta}r^2\sqrt{2}drd\theta$。计算得到$\frac{32}{9}\sqrt{2}$。