题目
求曲线^2+(y)^2+(z)^2=6,-|||-x+y+z=0在点(1,-2,1)处的切线及法平面方程.
求曲线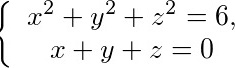 在点(1,-2,1)处的切线及法平面方程.
在点(1,-2,1)处的切线及法平面方程.
题目解答
答案
解 为求切向量,将所给方程的两边对x求导数,可得
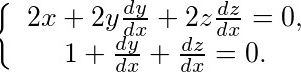
解方程组得
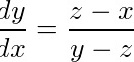 ,
,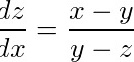 .
.
在点(1,-2,1)处,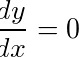 ,
,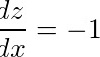 ,从而
,从而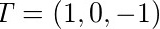 .
.
所求切线方程为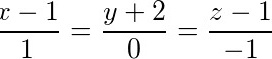 ,
,
法平面方程为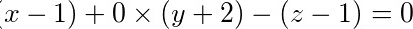 ,
,
即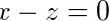 .
.
解析
考查要点:本题主要考查空间曲线在某一点处的切线方程和法平面方程的求解方法,涉及隐函数求导和几何向量的应用。
解题核心思路:
- 确定切线方向向量:通过联立方程的隐函数求导,得到曲线在给定点的切向量。
- 切线方程:利用点向式方程,结合切向量的方向分量写出。
- 法平面方程:以切向量为法向量,利用点法式方程求解。
破题关键点:
- 隐函数求导:对联立方程分别求导,建立关于$\frac{dy}{dx}$和$\frac{dz}{dx}$的方程组。
- 方向向量的几何意义:切向量由导数确定,法平面方程直接由切向量的分量构成。
步骤1:隐函数求导
对联立方程分别对$x$求导:
-
第一个方程:$x^{2}+y^{2}+z^{2}=6$
两边对$x$求导得:
$2x + 2y\frac{dy}{dx} + 2z\frac{dz}{dx} = 0 \quad \Rightarrow \quad x + y\frac{dy}{dx} + z\frac{dz}{dx} = 0.$ -
第二个方程:$x+y+z=0$
两边对$x$求导得:
$1 + \frac{dy}{dx} + \frac{dz}{dx} = 0.$
步骤2:解方程组求导数
将点$(1,-2,1)$代入方程组:
- 代入第一个方程:
$1 + (-2)\frac{dy}{dx} + 1\cdot\frac{dz}{dx} = 0 \quad \Rightarrow \quad -2\frac{dy}{dx} + \frac{dz}{dx} = -1.$ - 代入第二个方程:
$1 + \frac{dy}{dx} + \frac{dz}{dx} = 0 \quad \Rightarrow \quad \frac{dy}{dx} + \frac{dz}{dx} = -1.$
联立解方程:
- 从第二个方程得:$\frac{dz}{dx} = -1 - \frac{dy}{dx}.$
- 代入第一个方程:
$-2\frac{dy}{dx} + (-1 - \frac{dy}{dx}) = -1 \quad \Rightarrow \quad -3\frac{dy}{dx} = 0 \quad \Rightarrow \quad \frac{dy}{dx} = 0.$ - 回代得:$\frac{dz}{dx} = -1.$
步骤3:确定切向量与方程
- 切向量:$\mathbf{T} = \left(1, \frac{dy}{dx}, \frac{dz}{dx}\right) = (1, 0, -1).$
- 切线方程:
$\frac{x-1}{1} = \frac{y+2}{0} = \frac{z-1}{-1}.$
(注:分母为0时,对应项单独成立,即$y = -2$。) - 法平面方程:
切向量为法向量,方程为:
$(x-1) + 0 \cdot (y+2) - (z-1) = 0 \quad \Rightarrow \quad x - z = 0.$