题目
计算下列对弧长的曲线积分:-|||-(int )_(t)^2((x)^2+(y)^2)ds, 其中L为曲线 =a(cos t+tsin t), =a(sin t-tcos t)-|||-(0leqslant tleqslant 2pi ).

题目解答
答案
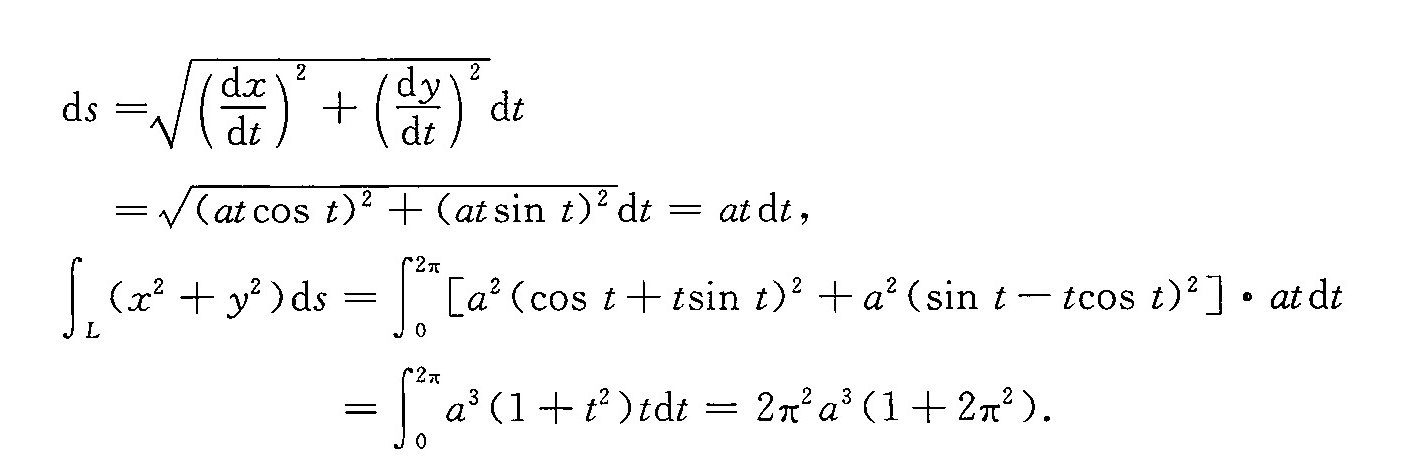
解析
步骤 1:计算 $ds$
根据曲线的参数方程 $x=a(\cos t+t\sin t)$ 和 $y=a(\sin t-t\cos t)$,我们首先计算 $ds$。$ds$ 是弧长微分,可以表示为 $ds=\sqrt{{(\frac{dx}{dt})}^{2}+{(\frac{dy}{dt})}^{2}}dt$。
步骤 2:计算 $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$
对 $x$ 和 $y$ 关于 $t$ 求导,得到 $\frac{dx}{dt}=a(-\sin t+\sin t+t\cos t)=at\cos t$ 和 $\frac{dy}{dt}=a(\cos t-\cos t+t\sin t)=at\sin t$。
步骤 3:代入 $ds$ 的表达式
将 $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$ 代入 $ds$ 的表达式中,得到 $ds=\sqrt{{(at\cos t)}^{2}+{(at\sin t)}^{2}}dt=\sqrt{a^2t^2(\cos^2 t+\sin^2 t)}dt=a|t|dt$。由于 $0\leqslant t\leqslant 2\pi$,$|t|=t$,所以 $ds=atdt$。
步骤 4:计算积分
将 $ds$ 和 $x^2+y^2$ 代入原积分中,得到 ${\int }_{L}({x}^{2}+{y}^{2})ds={\int }_{0}^{2\pi }[a^2(\cos^2 t+t^2\sin^2 t+2t\cos t\sin t)+a^2(\sin^2 t+t^2\cos^2 t-2t\cos t\sin t)]atdt$。化简后得到 ${\int }_{0}^{2\pi }a^3(1+t^2)tdt$。
步骤 5:计算定积分
计算定积分 ${\int }_{0}^{2\pi }a^3(1+t^2)tdt$,得到 $a^3\int_{0}^{2\pi}(t+t^3)dt=a^3[\frac{1}{2}t^2+\frac{1}{4}t^4]_{0}^{2\pi}=a^3(\frac{1}{2}(2\pi)^2+\frac{1}{4}(2\pi)^4)=a^3(2\pi^2+4\pi^4)$。
根据曲线的参数方程 $x=a(\cos t+t\sin t)$ 和 $y=a(\sin t-t\cos t)$,我们首先计算 $ds$。$ds$ 是弧长微分,可以表示为 $ds=\sqrt{{(\frac{dx}{dt})}^{2}+{(\frac{dy}{dt})}^{2}}dt$。
步骤 2:计算 $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$
对 $x$ 和 $y$ 关于 $t$ 求导,得到 $\frac{dx}{dt}=a(-\sin t+\sin t+t\cos t)=at\cos t$ 和 $\frac{dy}{dt}=a(\cos t-\cos t+t\sin t)=at\sin t$。
步骤 3:代入 $ds$ 的表达式
将 $\frac{dx}{dt}$ 和 $\frac{dy}{dt}$ 代入 $ds$ 的表达式中,得到 $ds=\sqrt{{(at\cos t)}^{2}+{(at\sin t)}^{2}}dt=\sqrt{a^2t^2(\cos^2 t+\sin^2 t)}dt=a|t|dt$。由于 $0\leqslant t\leqslant 2\pi$,$|t|=t$,所以 $ds=atdt$。
步骤 4:计算积分
将 $ds$ 和 $x^2+y^2$ 代入原积分中,得到 ${\int }_{L}({x}^{2}+{y}^{2})ds={\int }_{0}^{2\pi }[a^2(\cos^2 t+t^2\sin^2 t+2t\cos t\sin t)+a^2(\sin^2 t+t^2\cos^2 t-2t\cos t\sin t)]atdt$。化简后得到 ${\int }_{0}^{2\pi }a^3(1+t^2)tdt$。
步骤 5:计算定积分
计算定积分 ${\int }_{0}^{2\pi }a^3(1+t^2)tdt$,得到 $a^3\int_{0}^{2\pi}(t+t^3)dt=a^3[\frac{1}{2}t^2+\frac{1}{4}t^4]_{0}^{2\pi}=a^3(\frac{1}{2}(2\pi)^2+\frac{1}{4}(2\pi)^4)=a^3(2\pi^2+4\pi^4)$。