题目
1.用比较审敛法判别下列级数的敛散性.-|||-(1) sum _(n=1)^infty sin dfrac (pi )({n)^2}-|||-(2) sum _(n=1)^infty dfrac (1+n)(1+{n)^2}-|||-(3) sum _(n=1)^infty dfrac (1)(nsqrt {1+n)}-|||-(4) sum _(n=1)^infty dfrac (1)(ln (1+n))

题目解答
答案
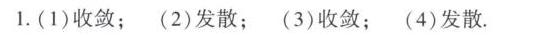
解析
(1) 步骤 1:比较级数
$\sin \dfrac {\pi }{{n}^{2}}$ 与 $\dfrac {\pi }{{n}^{2}}$ 进行比较,因为当 $n$ 足够大时,$\sin x \approx x$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {\pi }{{n}^{2}}$ 是一个 p-级数,其中 $p=2>1$,因此收敛。
步骤 3:结论
由于 $\sin \dfrac {\pi }{{n}^{2}} \leq \dfrac {\pi }{{n}^{2}}$,且 $\sum _{n=1}^{\infty }\dfrac {\pi }{{n}^{2}}$ 收敛,根据比较审敛法,$\sum _{n=1}^{\infty }\sin \dfrac {\pi }{{n}^{2}}$ 也收敛。
(2) 步骤 1:比较级数
$\dfrac {1+n}{1+{n}^{2}}$ 与 $\dfrac {1}{n}$ 进行比较,因为当 $n$ 足够大时,$\dfrac {1+n}{1+{n}^{2}} \approx \dfrac {1}{n}$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n}$ 是一个调和级数,发散。
步骤 3:结论
由于 $\dfrac {1+n}{1+{n}^{2}} \geq \dfrac {1}{n}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1+n}{1+{n}^{2}}$ 也发散。
(3) 步骤 1:比较级数
$\dfrac {1}{n\sqrt {1+n}}$ 与 $\dfrac {1}{n^{3/2}}$ 进行比较,因为当 $n$ 足够大时,$\dfrac {1}{n\sqrt {1+n}} \approx \dfrac {1}{n^{3/2}}$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n^{3/2}}$ 是一个 p-级数,其中 $p=3/2>1$,因此收敛。
步骤 3:结论
由于 $\dfrac {1}{n\sqrt {1+n}} \leq \dfrac {1}{n^{3/2}}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n^{3/2}}$ 收敛,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1}{n\sqrt {1+n}}$ 也收敛。
(4) 步骤 1:比较级数
$\dfrac {1}{\ln (1+n)}$ 与 $\dfrac {1}{n}$ 进行比较,因为当 $n$ 足够大时,$\ln (1+n) \approx \ln n$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n}$ 是一个调和级数,发散。
步骤 3:结论
由于 $\dfrac {1}{\ln (1+n)} \geq \dfrac {1}{n}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1}{\ln (1+n)}$ 也发散。
$\sin \dfrac {\pi }{{n}^{2}}$ 与 $\dfrac {\pi }{{n}^{2}}$ 进行比较,因为当 $n$ 足够大时,$\sin x \approx x$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {\pi }{{n}^{2}}$ 是一个 p-级数,其中 $p=2>1$,因此收敛。
步骤 3:结论
由于 $\sin \dfrac {\pi }{{n}^{2}} \leq \dfrac {\pi }{{n}^{2}}$,且 $\sum _{n=1}^{\infty }\dfrac {\pi }{{n}^{2}}$ 收敛,根据比较审敛法,$\sum _{n=1}^{\infty }\sin \dfrac {\pi }{{n}^{2}}$ 也收敛。
(2) 步骤 1:比较级数
$\dfrac {1+n}{1+{n}^{2}}$ 与 $\dfrac {1}{n}$ 进行比较,因为当 $n$ 足够大时,$\dfrac {1+n}{1+{n}^{2}} \approx \dfrac {1}{n}$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n}$ 是一个调和级数,发散。
步骤 3:结论
由于 $\dfrac {1+n}{1+{n}^{2}} \geq \dfrac {1}{n}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1+n}{1+{n}^{2}}$ 也发散。
(3) 步骤 1:比较级数
$\dfrac {1}{n\sqrt {1+n}}$ 与 $\dfrac {1}{n^{3/2}}$ 进行比较,因为当 $n$ 足够大时,$\dfrac {1}{n\sqrt {1+n}} \approx \dfrac {1}{n^{3/2}}$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n^{3/2}}$ 是一个 p-级数,其中 $p=3/2>1$,因此收敛。
步骤 3:结论
由于 $\dfrac {1}{n\sqrt {1+n}} \leq \dfrac {1}{n^{3/2}}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n^{3/2}}$ 收敛,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1}{n\sqrt {1+n}}$ 也收敛。
(4) 步骤 1:比较级数
$\dfrac {1}{\ln (1+n)}$ 与 $\dfrac {1}{n}$ 进行比较,因为当 $n$ 足够大时,$\ln (1+n) \approx \ln n$。
步骤 2:判断敛散性
$\sum _{n=1}^{\infty }\dfrac {1}{n}$ 是一个调和级数,发散。
步骤 3:结论
由于 $\dfrac {1}{\ln (1+n)} \geq \dfrac {1}{n}$,且 $\sum _{n=1}^{\infty }\dfrac {1}{n}$ 发散,根据比较审敛法,$\sum _{n=1}^{\infty }\dfrac {1}{\ln (1+n)}$ 也发散。