题目
已知(x)的一个原函数是sin2x,则(x)的一个原函数是sin2x ( )A. (x)的一个原函数是sin2x; B. (x)的一个原函数是sin2x; C. (x)的一个原函数是sin2x; D. (x)的一个原函数是sin2x。
已知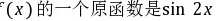 ,则
,则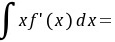 ( )
( )
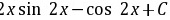 ;
;B.
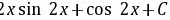 ;
;C.
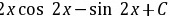 ;
;D.
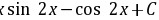 。
。题目解答
答案
C. $2x\cos 2x-\sin 2x+C$
解析
考查要点:本题主要考查分部积分法的应用,以及原函数与导数之间的关系。
解题思路:
- 确定$f(x)$:已知$f(x)$的原函数是$\sin 2x$,因此$f(x)$是$\sin 2x$的导数,即$f(x) = 2\cos 2x$。
- 应用分部积分法:对$\int x f'(x) \, dx$进行分部积分,选择$u = x$,$dv = f'(x) \, dx$,则$du = dx$,$v = f(x)$。
- 代入公式计算:分部积分公式为$\int u \, dv = uv - \int v \, du$,代入后化简即可得到结果。
步骤1:确定$f(x)$
已知$f(x)$的原函数是$\sin 2x$,因此:
$f(x) = \frac{d}{dx} (\sin 2x) = 2\cos 2x.$
步骤2:应用分部积分法
对$\int x f'(x) \, dx$进行分部积分,设:
$u = x \quad \Rightarrow \quad du = dx,$
$dv = f'(x) \, dx \quad \Rightarrow \quad v = f(x) = 2\cos 2x.$
根据分部积分公式:
$\begin{aligned}\int x f'(x) \, dx &= x \cdot f(x) - \int f(x) \, dx \\&= x \cdot 2\cos 2x - \int 2\cos 2x \, dx.\end{aligned}$
步骤3:计算剩余积分
计算$\int 2\cos 2x \, dx$:
$\int 2\cos 2x \, dx = 2 \cdot \frac{1}{2} \sin 2x + C = \sin 2x + C.$
步骤4:整理结果
将结果代入分部积分公式:
$\begin{aligned}\int x f'(x) \, dx &= 2x\cos 2x - (\sin 2x + C) \\&= 2x\cos 2x - \sin 2x + C.\end{aligned}$