题目
齐次线性方程组齐次线性方程组齐次线性方程组,齐次线性方程组齐次线性方程组(齐次线性方程组)
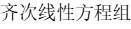
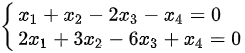
 ,
,
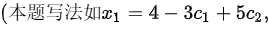
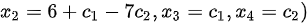
( )
)
题目解答
答案
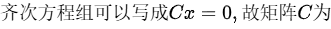
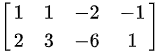 ,
,

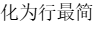
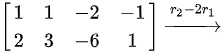
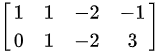
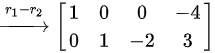 ,
,
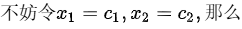
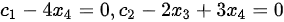
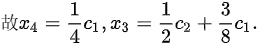
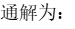
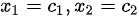 ,
,
解析
考查要点:本题主要考查齐次线性方程组的解法,特别是通过将系数矩阵化为行最简形来求通解的能力。
解题核心思路:
- 行最简形:通过初等行变换将系数矩阵化为行最简形,明确主变量与自由变量。
- 自由变量的设定:根据行最简形确定自由变量,用自由变量表示主变量。
- 通解的构造:将主变量用自由变量线性表示,最终写出通解形式。
破题关键点:
- 正确进行行变换:确保系数矩阵化为标准的行最简形。
- 区分主变量与自由变量:首1对应的变量为主变量,其余为自由变量。
- 参数化自由变量:通常设自由变量为独立参数,如$c_1, c_2$,进而表达主变量。
步骤1:写出系数矩阵并化为行最简形
原方程组的系数矩阵为:
$\begin{pmatrix}1 & 1 & -2 & -1 \\2 & 3 & -6 & 1\end{pmatrix}$
初等行变换过程:
-
消去第二行第一个元素:
$r_2 = r_2 - 2r_1$,得到:
$\begin{pmatrix} 1 & 1 & -2 & -1 \\ 0 & 1 & -2 & 3 \end{pmatrix}$ -
消去第一行第二个元素:
$r_1 = r_1 - r_2$,得到行最简形:
$C = \begin{pmatrix} 1 & 0 & 0 & -4 \\ 0 & 1 & -2 & 3 \end{pmatrix}$
步骤2:确定主变量与自由变量
- 主变量:对应首1的列,即$x_1$和$x_2$。
- 自由变量:未被首1占据的列,即$x_3$和$x_4$,设为参数$c_1, c_2$。
步骤3:用自由变量表示主变量
根据行最简形对应的方程组:
- 第一行:$x_1 - 4x_4 = 0 \Rightarrow x_1 = 4x_4 = 4c_2$。
- 第二行:$x_2 - 2x_3 + 3x_4 = 0 \Rightarrow x_2 = 2x_3 - 3x_4 = 2c_1 - 3c_2$。
步骤4:写出通解
将自由变量代入,通解为:
$\begin{cases}x_1 = 4c_2 \\x_2 = 2c_1 - 3c_2 \\x_3 = c_1 \\x_4 = c_2\end{cases}$