题目
一复杂的系统由个相互独立起作用的部件所组成.每个部件的可靠性(即部件正常工作的概率)为0.90.且必须至少有80%的部件工作才能使整个系统工作,问至少为多大才能使系统的可靠性不低于0.95。
一复杂的系统由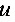 个相互独立起作用的部件所组成.每个部件的可靠性(即部件正常工作的概率)为0.90.且必须至少有80%的部件工作才能使整个系统工作,问
个相互独立起作用的部件所组成.每个部件的可靠性(即部件正常工作的概率)为0.90.且必须至少有80%的部件工作才能使整个系统工作,问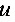 至少为多大才能使系统的可靠性不低于0.95。
至少为多大才能使系统的可靠性不低于0.95。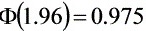
题目解答
答案
解:(1)正常工作部件数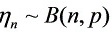 ,
,
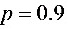 ,
, 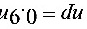 ,
, 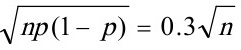
(2) 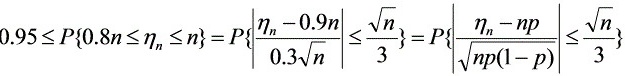
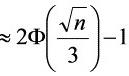 , 即
, 即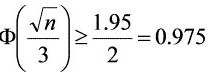 ,查表,得
,查表,得
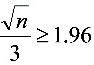 ,
,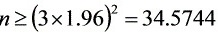 . 取
. 取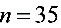 .
.
(3)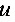 至少为35才能使系统的可靠性不低于0.95.
至少为35才能使系统的可靠性不低于0.95.
解析
步骤 1:定义随机变量
设正常工作的部件数为$X$,则$X$服从二项分布$B(n,0.9)$,其中$n$为部件总数,$0.9$为每个部件正常工作的概率。
步骤 2:计算期望和方差
根据二项分布的性质,$X$的期望$E(X)=np=0.9n$,方差$Var(X)=np(1-p)=0.9n(1-0.9)=0.09n$。
步骤 3:应用中心极限定理
当$n$足够大时,$X$近似服从正态分布$N(0.9n,0.09n)$。为了使系统正常工作,至少需要$0.8n$个部件正常工作,即$X\geqslant 0.8n$。
步骤 4:计算概率
根据正态分布的性质,$P(X\geqslant 0.8n)=P(\dfrac {X-0.9n}{\sqrt {0.09n}}\geqslant \dfrac {0.8n-0.9n}{\sqrt {0.09n}})=P(Z\geqslant \dfrac {-0.1n}{\sqrt {0.09n}})=P(Z\geqslant -\dfrac {\sqrt {n}}{3})$,其中$Z$为标准正态分布。
步骤 5:求解$n$
根据题目要求,$P(Z\geqslant -\dfrac {\sqrt {n}}{3})\geqslant 0.95$,即$P(Z\leqslant \dfrac {\sqrt {n}}{3})\geqslant 0.95$。查标准正态分布表,得$\dfrac {\sqrt {n}}{3}\geqslant 1.96$,解得$n\geqslant {(3\times 1.96)}^{2}=34.5744$。取$n=35$。
设正常工作的部件数为$X$,则$X$服从二项分布$B(n,0.9)$,其中$n$为部件总数,$0.9$为每个部件正常工作的概率。
步骤 2:计算期望和方差
根据二项分布的性质,$X$的期望$E(X)=np=0.9n$,方差$Var(X)=np(1-p)=0.9n(1-0.9)=0.09n$。
步骤 3:应用中心极限定理
当$n$足够大时,$X$近似服从正态分布$N(0.9n,0.09n)$。为了使系统正常工作,至少需要$0.8n$个部件正常工作,即$X\geqslant 0.8n$。
步骤 4:计算概率
根据正态分布的性质,$P(X\geqslant 0.8n)=P(\dfrac {X-0.9n}{\sqrt {0.09n}}\geqslant \dfrac {0.8n-0.9n}{\sqrt {0.09n}})=P(Z\geqslant \dfrac {-0.1n}{\sqrt {0.09n}})=P(Z\geqslant -\dfrac {\sqrt {n}}{3})$,其中$Z$为标准正态分布。
步骤 5:求解$n$
根据题目要求,$P(Z\geqslant -\dfrac {\sqrt {n}}{3})\geqslant 0.95$,即$P(Z\leqslant \dfrac {\sqrt {n}}{3})\geqslant 0.95$。查标准正态分布表,得$\dfrac {\sqrt {n}}{3}\geqslant 1.96$,解得$n\geqslant {(3\times 1.96)}^{2}=34.5744$。取$n=35$。