题目
求过点A(1,2,1 ),而与两直线 L1: =dfrac {y-2)(1)=dfrac (z-1)(1) 平行的平面方程.

题目解答
答案

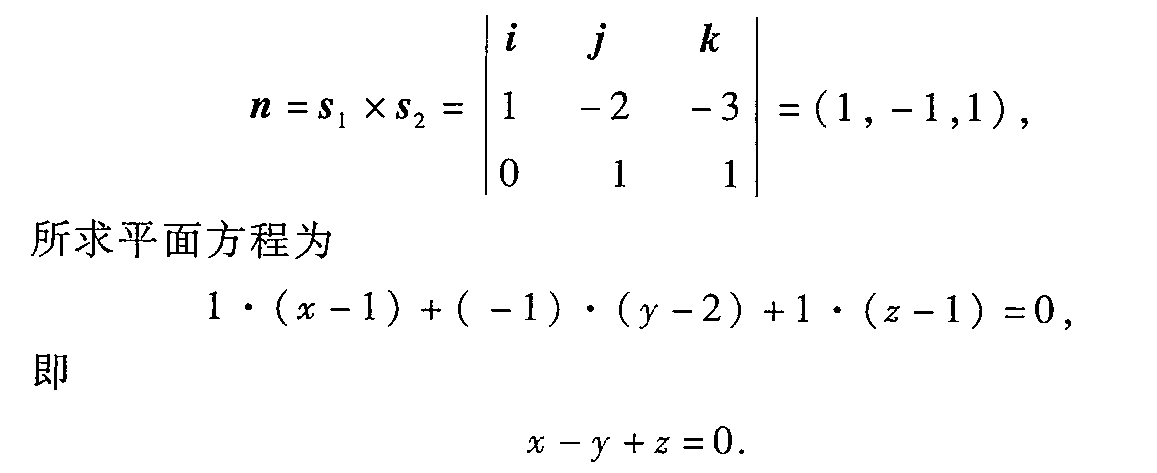
解析
步骤 1:确定直线 L1 的方向向量
直线 L1 的方程为 $\left \{ \begin{matrix} x+2y-z+1=0\\ x-y+z-1=0\end{matrix} \right.$,我们可以通过求解这两个平面的法向量的叉积来得到直线 L1 的方向向量。设这两个平面的法向量分别为 $\vec{n_1} = (1, 2, -1)$ 和 $\vec{n_2} = (1, -1, 1)$,则直线 L1 的方向向量 $\vec{S_1} = \vec{n_1} \times \vec{n_2}$。
步骤 2:计算直线 L1 的方向向量
$\vec{S_1} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 2 & -1 \\ 1 & -1 & 1 \end{vmatrix} = (2 \cdot 1 - (-1) \cdot (-1))\vec{i} - (1 \cdot 1 - (-1) \cdot 1)\vec{j} + (1 \cdot (-1) - 2 \cdot 1)\vec{k} = (2 - 1)\vec{i} - (1 + 1)\vec{j} + (-1 - 2)\vec{k} = (1, -2, -3)$。
步骤 3:确定直线 L2 的方向向量
直线 L2 的方程为 $\dfrac {x}{0}=\dfrac {y-2}{1}=\dfrac {z-1}{1}$,其方向向量为 $\vec{S_2} = (0, 1, 1)$。
步骤 4:计算所求平面的法向量
所求平面的法向量 $\vec{n} = \vec{S_1} \times \vec{S_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & -2 & -3 \\ 0 & 1 & 1 \end{vmatrix} = ((-2) \cdot 1 - (-3) \cdot 1)\vec{i} - (1 \cdot 1 - (-3) \cdot 0)\vec{j} + (1 \cdot 1 - (-2) \cdot 0)\vec{k} = (-2 + 3)\vec{i} - (1 + 0)\vec{j} + (1 + 0)\vec{k} = (1, -1, 1)$。
步骤 5:确定所求平面的方程
所求平面的方程为 $\vec{n} \cdot (\vec{r} - \vec{r_0}) = 0$,其中 $\vec{r_0} = (1, 2, 1)$,$\vec{r} = (x, y, z)$,$\vec{n} = (1, -1, 1)$。代入得 $(1, -1, 1) \cdot (x - 1, y - 2, z - 1) = 0$,即 $x - 1 - (y - 2) + (z - 1) = 0$,化简得 $x - y + z = 0$。
直线 L1 的方程为 $\left \{ \begin{matrix} x+2y-z+1=0\\ x-y+z-1=0\end{matrix} \right.$,我们可以通过求解这两个平面的法向量的叉积来得到直线 L1 的方向向量。设这两个平面的法向量分别为 $\vec{n_1} = (1, 2, -1)$ 和 $\vec{n_2} = (1, -1, 1)$,则直线 L1 的方向向量 $\vec{S_1} = \vec{n_1} \times \vec{n_2}$。
步骤 2:计算直线 L1 的方向向量
$\vec{S_1} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & 2 & -1 \\ 1 & -1 & 1 \end{vmatrix} = (2 \cdot 1 - (-1) \cdot (-1))\vec{i} - (1 \cdot 1 - (-1) \cdot 1)\vec{j} + (1 \cdot (-1) - 2 \cdot 1)\vec{k} = (2 - 1)\vec{i} - (1 + 1)\vec{j} + (-1 - 2)\vec{k} = (1, -2, -3)$。
步骤 3:确定直线 L2 的方向向量
直线 L2 的方程为 $\dfrac {x}{0}=\dfrac {y-2}{1}=\dfrac {z-1}{1}$,其方向向量为 $\vec{S_2} = (0, 1, 1)$。
步骤 4:计算所求平面的法向量
所求平面的法向量 $\vec{n} = \vec{S_1} \times \vec{S_2} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ 1 & -2 & -3 \\ 0 & 1 & 1 \end{vmatrix} = ((-2) \cdot 1 - (-3) \cdot 1)\vec{i} - (1 \cdot 1 - (-3) \cdot 0)\vec{j} + (1 \cdot 1 - (-2) \cdot 0)\vec{k} = (-2 + 3)\vec{i} - (1 + 0)\vec{j} + (1 + 0)\vec{k} = (1, -1, 1)$。
步骤 5:确定所求平面的方程
所求平面的方程为 $\vec{n} \cdot (\vec{r} - \vec{r_0}) = 0$,其中 $\vec{r_0} = (1, 2, 1)$,$\vec{r} = (x, y, z)$,$\vec{n} = (1, -1, 1)$。代入得 $(1, -1, 1) \cdot (x - 1, y - 2, z - 1) = 0$,即 $x - 1 - (y - 2) + (z - 1) = 0$,化简得 $x - y + z = 0$。