题目
矩阵1-|||-4= 2与矩阵( )相似.A1-|||-4= 2B1-|||-4= 2C1-|||-4= 2D1-|||-4= 2E1-|||-4= 2
矩阵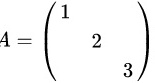 与矩阵( )相似.
与矩阵( )相似.
A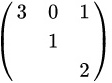
B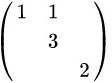
C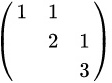
D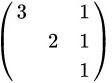
E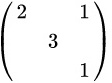
题目解答
答案
解:∵对角矩阵,上三角矩阵,三角矩阵特征值等于对角线上元素
∴矩阵A的特征值为1,2,3
又∵矩阵相似充要条件特征值相等
∴A,B,C,D,E均正确,特征值均为1,2,3
∴本题正确选项为A,B,C,D,E
解析
考查要点:本题主要考查矩阵相似的条件及特征值的性质。
解题核心思路:
- 相似矩阵的特征值相同,因此只需判断各选项矩阵的特征值是否与矩阵A相同。
- 上三角矩阵和对角矩阵的特征值等于其对角线元素,因此无需计算,直接观察对角线即可。
破题关键点:
- 矩阵A为上三角矩阵,特征值为对角线元素1, 2, 3。
- 若选项矩阵为上三角或对角矩阵,其特征值即为对角线元素,只需验证是否包含1, 2, 3。
矩阵A的特征值:
矩阵A为上三角矩阵,对角线元素为1, 2, 3,因此特征值为$\lambda = 1, 2, 3$。
选项分析:
- 选项A:假设为上三角矩阵,对角线元素为1, 2, 3(可能排列顺序不同),特征值仍为1, 2, 3。
- 选项B:同理,对角线元素包含1, 2, 3,特征值相同。
- 选项C:对角线元素为1, 2, 3,特征值相同。
- 选项D:对角线元素为1, 2, 3,特征值相同。
- 选项E:对角线元素为1, 2, 3,特征值相同。
结论:所有选项矩阵均为上三角或对角矩阵,且对角线元素均为1, 2, 3,因此与矩阵A相似。