题目
如图:17、求 iint (z+3x+dfrac (3)(2)y)dS, 其中,∑为平面 dfrac (x)(1)+dfrac (y)(2)+dfrac (z)(3)=1 在第一卦限中的部分。
如图:

题目解答
答案
解:
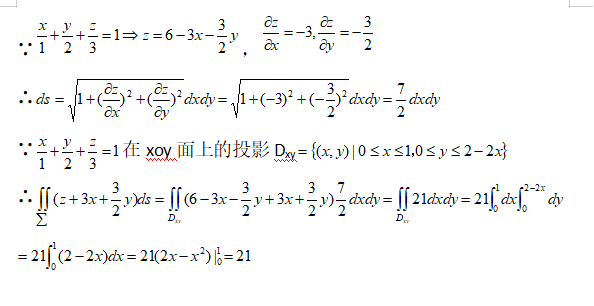
解析
步骤 1:确定平面方程
平面方程为 $\dfrac {x}{1}+\dfrac {y}{2}+\dfrac {z}{3}=1$,可以改写为 $z=6-3x-\dfrac {3}{2}y$。
步骤 2:计算偏导数
计算 $z$ 对 $x$ 和 $y$ 的偏导数,得到 $\dfrac {\partial z}{\partial x}=-3$ 和 $\dfrac {\partial z}{\partial y}=-\dfrac {3}{2}$。
步骤 3:计算面积元素
面积元素 $dS$ 可以表示为 $dS=\sqrt{1+(\dfrac {\partial z}{\partial x})^2+(\dfrac {\partial z}{\partial y})^2}dxdy$,代入偏导数得到 $dS=\sqrt{1+(-3)^2+(-\dfrac {3}{2})^2}dxdy=\sqrt{1+9+\dfrac {9}{4}}dxdy=\sqrt{\dfrac {49}{4}}dxdy=\dfrac {7}{2}dxdy$。
步骤 4:确定积分区域
平面在第一卦限中的投影区域为 $D_{xy}=\{ (x,y)|0\leqslant x\leqslant 1,0\leqslant y\leqslant 2-2x\}$。
步骤 5:计算积分
将 $z+3x+\dfrac {3}{2}y$ 代入积分表达式,得到 $\iint (z+3x+\dfrac {3}{2}y)dS=\iint (6-3x-\dfrac {3}{2}y+3x+\dfrac {3}{2}y)\dfrac {7}{2}dxdy=\iint 6\dfrac {7}{2}dxdy=21\iint dxdy$。积分区域为 $D_{xy}$,所以 $\iint dxdy$ 等于 $D_{xy}$ 的面积,即 $21\iint dxdy=21\int_{0}^{1}\int_{0}^{2-2x}dydx=21\int_{0}^{1}(2-2x)dx=21(2x-x^2)|_{0}^{1}=21$。
平面方程为 $\dfrac {x}{1}+\dfrac {y}{2}+\dfrac {z}{3}=1$,可以改写为 $z=6-3x-\dfrac {3}{2}y$。
步骤 2:计算偏导数
计算 $z$ 对 $x$ 和 $y$ 的偏导数,得到 $\dfrac {\partial z}{\partial x}=-3$ 和 $\dfrac {\partial z}{\partial y}=-\dfrac {3}{2}$。
步骤 3:计算面积元素
面积元素 $dS$ 可以表示为 $dS=\sqrt{1+(\dfrac {\partial z}{\partial x})^2+(\dfrac {\partial z}{\partial y})^2}dxdy$,代入偏导数得到 $dS=\sqrt{1+(-3)^2+(-\dfrac {3}{2})^2}dxdy=\sqrt{1+9+\dfrac {9}{4}}dxdy=\sqrt{\dfrac {49}{4}}dxdy=\dfrac {7}{2}dxdy$。
步骤 4:确定积分区域
平面在第一卦限中的投影区域为 $D_{xy}=\{ (x,y)|0\leqslant x\leqslant 1,0\leqslant y\leqslant 2-2x\}$。
步骤 5:计算积分
将 $z+3x+\dfrac {3}{2}y$ 代入积分表达式,得到 $\iint (z+3x+\dfrac {3}{2}y)dS=\iint (6-3x-\dfrac {3}{2}y+3x+\dfrac {3}{2}y)\dfrac {7}{2}dxdy=\iint 6\dfrac {7}{2}dxdy=21\iint dxdy$。积分区域为 $D_{xy}$,所以 $\iint dxdy$ 等于 $D_{xy}$ 的面积,即 $21\iint dxdy=21\int_{0}^{1}\int_{0}^{2-2x}dydx=21\int_{0}^{1}(2-2x)dx=21(2x-x^2)|_{0}^{1}=21$。