题目
0 a 0-|||-设A= 1 0 1 为反对称矩阵,则必有-|||-b c 0a=b=-1,c=0 . a=c=-1,b=0 a=c=0,b=-1 . b=c=-1,a=0.
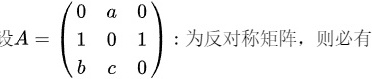
a=b=-1,c=0 .
a=c=-1,b=0
a=c=0,b=-1 .
b=c=-1,a=0.
题目解答
答案
要求矩阵 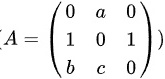 是反对称矩阵,意味着 (
是反对称矩阵,意味着 (  ).
).
计算 ( ):
):
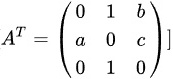
要求 ( 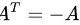 ):
):
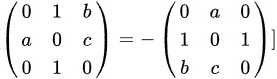
比较每个对应元素:
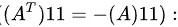
[ 0 = 0 ]
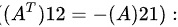
[ 1 = -a ]
从中得到 ( a = -1 ).
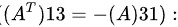
[ b = 0 ]
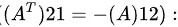
[ a = -1 ]
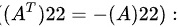
[ 0 = 0 ]
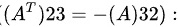
[ c = -1 ]
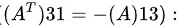
[ 0 = b ]
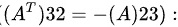
[ 1 = -c ]
从中得到 ( c = -1 ).
综上所述,要使矩阵 ( A ) 成为反对称矩阵,必须满足 ( a = -1 ), ( b = 0 ), ( c = -1 ).
解析
步骤 1:定义反对称矩阵
一个矩阵 $A$ 是反对称矩阵,当且仅当 $A^T = -A$,其中 $A^T$ 是矩阵 $A$ 的转置矩阵。
步骤 2:计算矩阵 $A$ 的转置矩阵 $A^T$
给定矩阵 $A = \left (\begin{matrix} 0& a& 0\\ 1& 0& 1\\ b& c& 0\end{matrix} ) \right.$,其转置矩阵 $A^T$ 为:
$$
A^T = \left (\begin{matrix} 0& 1& b\\ a& 0& c\\ 0& 1& 0\end{matrix} ) \right.
$$
步骤 3:根据反对称矩阵的定义,比较 $A^T$ 和 $-A$
根据定义,$A^T = -A$,即:
$$
\left (\begin{matrix} 0& 1& b\\ a& 0& c\\ 0& 1& 0\end{matrix} ) \right. = -\left (\begin{matrix} 0& a& 0\\ 1& 0& 1\\ b& c& 0\end{matrix} ) \right.
$$
计算 $-A$:
$$
-A = \left (\begin{matrix} 0& -a& 0\\ -1& 0& -1\\ -b& -c& 0\end{matrix} ) \right.
$$
步骤 4:比较矩阵 $A^T$ 和 $-A$ 的对应元素
比较矩阵 $A^T$ 和 $-A$ 的对应元素,得到以下方程组:
$$
\begin{cases}
0 = 0 \\
1 = -a \\
b = -b \\
a = -1 \\
0 = 0 \\
c = -1 \\
0 = -1 \\
1 = -c \\
0 = 0
\end{cases}
$$
从方程组中解出 $a$、$b$ 和 $c$:
$$
\begin{cases}
1 = -a \Rightarrow a = -1 \\
b = -b \Rightarrow b = 0 \\
c = -1
\end{cases}
$$
一个矩阵 $A$ 是反对称矩阵,当且仅当 $A^T = -A$,其中 $A^T$ 是矩阵 $A$ 的转置矩阵。
步骤 2:计算矩阵 $A$ 的转置矩阵 $A^T$
给定矩阵 $A = \left (\begin{matrix} 0& a& 0\\ 1& 0& 1\\ b& c& 0\end{matrix} ) \right.$,其转置矩阵 $A^T$ 为:
$$
A^T = \left (\begin{matrix} 0& 1& b\\ a& 0& c\\ 0& 1& 0\end{matrix} ) \right.
$$
步骤 3:根据反对称矩阵的定义,比较 $A^T$ 和 $-A$
根据定义,$A^T = -A$,即:
$$
\left (\begin{matrix} 0& 1& b\\ a& 0& c\\ 0& 1& 0\end{matrix} ) \right. = -\left (\begin{matrix} 0& a& 0\\ 1& 0& 1\\ b& c& 0\end{matrix} ) \right.
$$
计算 $-A$:
$$
-A = \left (\begin{matrix} 0& -a& 0\\ -1& 0& -1\\ -b& -c& 0\end{matrix} ) \right.
$$
步骤 4:比较矩阵 $A^T$ 和 $-A$ 的对应元素
比较矩阵 $A^T$ 和 $-A$ 的对应元素,得到以下方程组:
$$
\begin{cases}
0 = 0 \\
1 = -a \\
b = -b \\
a = -1 \\
0 = 0 \\
c = -1 \\
0 = -1 \\
1 = -c \\
0 = 0
\end{cases}
$$
从方程组中解出 $a$、$b$ 和 $c$:
$$
\begin{cases}
1 = -a \Rightarrow a = -1 \\
b = -b \Rightarrow b = 0 \\
c = -1
\end{cases}
$$