题目
设函数f(x)= ) (x)^2, xleqslant 1 ax+b, xgt 1 .应取什么值？
设函数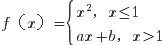
，为了使函数,
在
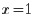处连续且可导，
应取什么值？
题目解答
答案
设函数f(x)={x平方,x≤1},{ax+b,x＞1},为了使函数f(x)在x=1处连续且可导,a、b应取什么值?
为使函数f(x)在x=1处连续
x≤1,f(x)=x^2,x=1时,f(1)=1
x>1, f(x)=ax+b,x从1+方向趋近于1时,f(x）=ax+b 应该趋近于1
即a+b趋近于1,a+b=1
“可导”的含义比“连续”的含义更多一层要求：要求在x=1处,x从左边趋近于1的极限（左极限）要求存在、并且等于函数在x=1的值f(1),而且x从右边趋近于1时的极限（右极限）也要求存在、并且等于函数在x=1的值f(1),这样才称得上“函数在x=1处可导”.
为了让左右极限相等、并且等于f(1)的值1,考察左极限在x=1的变化趋势,即f(x)=x^2在x=1处的切线方向,由f'(x)=2x决定.此切线的斜率k=2.
x从右边趋近于1时的极限（右极限）也应该具有斜率k=2的斜率.
当x>1时,f(x)=kx+h
因为已知 f(x)=ax+b
则 a=k=2,b=h,f(x)=2x+b
当x从右边趋近于1时,右极限等于左极限1及f(1)=1
故 2*1+b=1
b=-1.
结论：为了使函数f(x)在x=1处连续且可导,a、b应取a=2,b=-1.
为使函数f(x)在x=1处连续
x≤1,f(x)=x^2,x=1时,f(1)=1
x>1, f(x)=ax+b,x从1+方向趋近于1时,f(x）=ax+b 应该趋近于1
即a+b趋近于1,a+b=1
“可导”的含义比“连续”的含义更多一层要求：要求在x=1处,x从左边趋近于1的极限（左极限）要求存在、并且等于函数在x=1的值f(1),而且x从右边趋近于1时的极限（右极限）也要求存在、并且等于函数在x=1的值f(1),这样才称得上“函数在x=1处可导”.
为了让左右极限相等、并且等于f(1)的值1,考察左极限在x=1的变化趋势,即f(x)=x^2在x=1处的切线方向,由f'(x)=2x决定.此切线的斜率k=2.
x从右边趋近于1时的极限（右极限）也应该具有斜率k=2的斜率.
当x>1时,f(x)=kx+h
因为已知 f(x)=ax+b
则 a=k=2,b=h,f(x)=2x+b
当x从右边趋近于1时,右极限等于左极限1及f(1)=1
故 2*1+b=1
b=-1.
结论：为了使函数f(x)在x=1处连续且可导,a、b应取a=2,b=-1.
解析
步骤 1：确定函数在x=1处连续的条件
为了使函数f(x)在x=1处连续，需要满足f(1)的左极限等于f(1)的右极限，即：
$$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1)$$
由于f(x)在x≤1时为$x^2$，在x>1时为ax+b，因此：
$$\lim_{x \to 1^-} f(x) = 1^2 = 1$$
$$\lim_{x \to 1^+} f(x) = a \cdot 1 + b = a + b$$
所以，为了使函数在x=1处连续，需要满足：
$$a + b = 1$$
步骤 2：确定函数在x=1处可导的条件
为了使函数f(x)在x=1处可导，需要满足f(x)在x=1处的左导数等于右导数，即：
$$\lim_{x \to 1^-} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^+} \frac{f(x) - f(1)}{x - 1}$$
由于f(x)在x≤1时为$x^2$，在x>1时为ax+b，因此：
$$\lim_{x \to 1^-} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^-} \frac{x^2 - 1}{x - 1} = \lim_{x \to 1^-} (x + 1) = 2$$
$$\lim_{x \to 1^+} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^+} \frac{ax + b - 1}{x - 1} = \lim_{x \to 1^+} \frac{a(x - 1) + (a + b - 1)}{x - 1} = a$$
所以，为了使函数在x=1处可导，需要满足：
$$a = 2$$
步骤 3：求解a和b的值
根据步骤1和步骤2，我们得到两个方程：
$$a + b = 1$$
$$a = 2$$
将a=2代入第一个方程，得到：
$$2 + b = 1$$
解得：
$$b = -1$$
为了使函数f(x)在x=1处连续，需要满足f(1)的左极限等于f(1)的右极限，即：
$$\lim_{x \to 1^-} f(x) = \lim_{x \to 1^+} f(x) = f(1)$$
由于f(x)在x≤1时为$x^2$，在x>1时为ax+b，因此：
$$\lim_{x \to 1^-} f(x) = 1^2 = 1$$
$$\lim_{x \to 1^+} f(x) = a \cdot 1 + b = a + b$$
所以，为了使函数在x=1处连续，需要满足：
$$a + b = 1$$
步骤 2：确定函数在x=1处可导的条件
为了使函数f(x)在x=1处可导，需要满足f(x)在x=1处的左导数等于右导数，即：
$$\lim_{x \to 1^-} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^+} \frac{f(x) - f(1)}{x - 1}$$
由于f(x)在x≤1时为$x^2$，在x>1时为ax+b，因此：
$$\lim_{x \to 1^-} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^-} \frac{x^2 - 1}{x - 1} = \lim_{x \to 1^-} (x + 1) = 2$$
$$\lim_{x \to 1^+} \frac{f(x) - f(1)}{x - 1} = \lim_{x \to 1^+} \frac{ax + b - 1}{x - 1} = \lim_{x \to 1^+} \frac{a(x - 1) + (a + b - 1)}{x - 1} = a$$
所以，为了使函数在x=1处可导，需要满足：
$$a = 2$$
步骤 3：求解a和b的值
根据步骤1和步骤2，我们得到两个方程：
$$a + b = 1$$
$$a = 2$$
将a=2代入第一个方程，得到：
$$2 + b = 1$$
解得：
$$b = -1$$