题目
17.问λ取何值时,齐次线性方程组 ) (lambda +1)(x)_(1)+(x)_(2)+(x)_(3)=0, (x)_(1)+(lambda +1)(x)_(2)+(x)_(3)=0, (x)_(1)+(x)_(2)+(lambda +1)(x)_(3)=0 . ,有非零解?
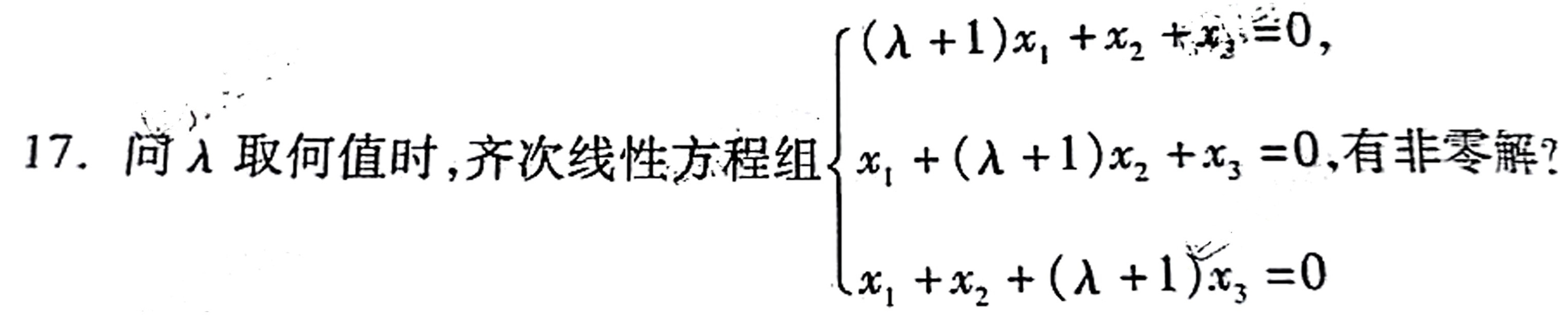
题目解答
答案

解析
步骤 1:写出系数矩阵
齐次线性方程组的系数矩阵为:
$$
A = \begin{pmatrix}
\lambda + 1 & 1 & 1 \\
1 & \lambda + 1 & 1 \\
1 & 1 & \lambda + 1
\end{pmatrix}
$$
步骤 2:计算行列式
为了使方程组有非零解,系数矩阵的行列式必须为零。计算行列式:
$$
\det(A) = \begin{vmatrix}
\lambda + 1 & 1 & 1 \\
1 & \lambda + 1 & 1 \\
1 & 1 & \lambda + 1
\end{vmatrix}
$$
步骤 3:展开行列式
利用行列式的性质,进行展开:
$$
\det(A) = (\lambda + 1) \begin{vmatrix}
\lambda + 1 & 1 \\
1 & \lambda + 1
\end{vmatrix} - 1 \begin{vmatrix}
1 & 1 \\
1 & \lambda + 1
\end{vmatrix} + 1 \begin{vmatrix}
1 & \lambda + 1 \\
1 & 1
\end{vmatrix}
$$
$$
= (\lambda + 1) \left( (\lambda + 1)^2 - 1 \right) - 1 \left( \lambda + 1 - 1 \right) + 1 \left( 1 - (\lambda + 1) \right)
$$
$$
= (\lambda + 1) \left( \lambda^2 + 2\lambda + 1 - 1 \right) - \lambda + 1 - \lambda
$$
$$
= (\lambda + 1) \left( \lambda^2 + 2\lambda \right) - 2\lambda
$$
$$
= (\lambda + 1) \lambda (\lambda + 2) - 2\lambda
$$
$$
= \lambda (\lambda + 1) (\lambda + 2) - 2\lambda
$$
$$
= \lambda (\lambda^2 + 3\lambda + 2 - 2)
$$
$$
= \lambda (\lambda^2 + 3\lambda)
$$
$$
= \lambda^2 (\lambda + 3)
$$
步骤 4:求解行列式为零的条件
为了使方程组有非零解,行列式必须为零:
$$
\lambda^2 (\lambda + 3) = 0
$$
解得:
$$
\lambda = 0 \quad \text{或} \quad \lambda = -3
$$
齐次线性方程组的系数矩阵为:
$$
A = \begin{pmatrix}
\lambda + 1 & 1 & 1 \\
1 & \lambda + 1 & 1 \\
1 & 1 & \lambda + 1
\end{pmatrix}
$$
步骤 2:计算行列式
为了使方程组有非零解,系数矩阵的行列式必须为零。计算行列式:
$$
\det(A) = \begin{vmatrix}
\lambda + 1 & 1 & 1 \\
1 & \lambda + 1 & 1 \\
1 & 1 & \lambda + 1
\end{vmatrix}
$$
步骤 3:展开行列式
利用行列式的性质,进行展开:
$$
\det(A) = (\lambda + 1) \begin{vmatrix}
\lambda + 1 & 1 \\
1 & \lambda + 1
\end{vmatrix} - 1 \begin{vmatrix}
1 & 1 \\
1 & \lambda + 1
\end{vmatrix} + 1 \begin{vmatrix}
1 & \lambda + 1 \\
1 & 1
\end{vmatrix}
$$
$$
= (\lambda + 1) \left( (\lambda + 1)^2 - 1 \right) - 1 \left( \lambda + 1 - 1 \right) + 1 \left( 1 - (\lambda + 1) \right)
$$
$$
= (\lambda + 1) \left( \lambda^2 + 2\lambda + 1 - 1 \right) - \lambda + 1 - \lambda
$$
$$
= (\lambda + 1) \left( \lambda^2 + 2\lambda \right) - 2\lambda
$$
$$
= (\lambda + 1) \lambda (\lambda + 2) - 2\lambda
$$
$$
= \lambda (\lambda + 1) (\lambda + 2) - 2\lambda
$$
$$
= \lambda (\lambda^2 + 3\lambda + 2 - 2)
$$
$$
= \lambda (\lambda^2 + 3\lambda)
$$
$$
= \lambda^2 (\lambda + 3)
$$
步骤 4:求解行列式为零的条件
为了使方程组有非零解,行列式必须为零:
$$
\lambda^2 (\lambda + 3) = 0
$$
解得:
$$
\lambda = 0 \quad \text{或} \quad \lambda = -3
$$