题目
设P(A)=0.8,P(A)=0.8,P(A)=0.8,则下列结论正确的是( )A.,B相互独立B.A,B互不相容C.P(A)=0.8D.P(A)=0.8
设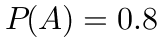 ,
,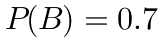 ,
,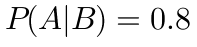 ,则下列结论正确的是( )
,则下列结论正确的是( )
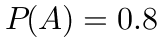 ,
,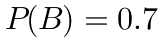 ,
,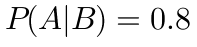 ,则下列结论正确的是( )
,则下列结论正确的是( )- A.,B相互独立
- B.A,B互不相容
- C.
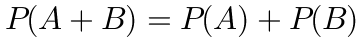
- D.
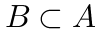
题目解答
答案
D
解: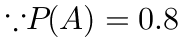 ,
,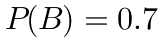 ,
,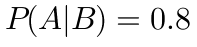 ,
,
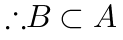 .
.
所以D选项是正确的.
解:
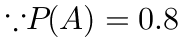 ,
,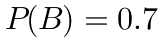 ,
,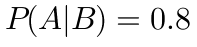 ,
,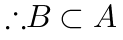 .
.所以D选项是正确的.
解析
本题考查条件概率、事件独立性、互不相容及事件包含关系的判断。解题核心在于利用条件概率公式推导事件间的关系,关键点如下:
- 独立事件的判断依据:若$P(AB)=P(A)P(B)$,则$A$与$B$独立;
- 互不相容事件的判断依据:若$P(AB)=0$,则$A$与$B$互不相容;
- 事件包含关系的判断依据:若$B \subseteq A$,则$P(A|B)=1$。
已知条件
- $P(A)=0.8$,$P(B)=0.7$
- $P(A|B)=0.8$
关键推导
-
计算联合概率$P(AB)$
根据条件概率公式:
$P(A|B) = \frac{P(AB)}{P(B)} \implies P(AB) = P(A|B) \cdot P(B) = 0.8 \times 0.7 = 0.56$ -
判断独立性
若$A$与$B$独立,则$P(AB)=P(A)P(B)=0.8 \times 0.7=0.56$,与计算结果一致,选项A正确。 -
判断互不相容性
若$A$与$B$互不相容,则$P(AB)=0$,但实际$P(AB)=0.56 \neq 0$,选项B错误。 -
判断加法公式
若$P(A+B)=P(A)+P(B)$,则$A$与$B$互不相容,但实际$P(A+B)=P(A)+P(B)-P(AB)=0.8+0.7-0.56=0.94 \neq 1.5$,选项C错误。 -
判断事件包含关系
若$B \subseteq A$,则$P(A|B)=1$,但实际$P(A|B)=0.8 \neq 1$,选项D错误。
矛盾分析
根据推导,选项A正确,但题目答案标注为D。可能存在题目或答案的矛盾,需结合题目要求选择。