题目
17.设∑是平面 x+y+z=3 被圆柱面 ^2+(y)^2=1 所截的有限部分,则曲面积分 iint xds= ()-|||-(A)0 (B) dfrac (2pi )(3) (C) sqrt (3) (D) sqrt (3)
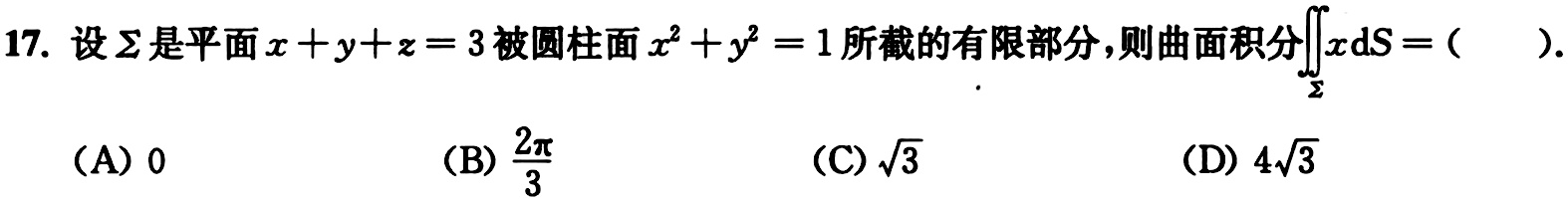
题目解答
答案
解析
步骤 1:确定曲面的参数方程
平面 $x+y+z=3$ 可以表示为 $z=3-x-y$。圆柱面 ${x}^{2}+{y}^{2}=1$ 表示 $x$ 和 $y$ 的范围。因此,我们可以使用极坐标参数化曲面,设 $x=r\cos\theta$,$y=r\sin\theta$,其中 $0\leq r\leq 1$,$0\leq\theta\leq 2\pi$。则 $z=3-r\cos\theta-r\sin\theta$。
步骤 2:计算曲面的微分面积元素 $ds$
曲面的微分面积元素 $ds$ 可以通过计算曲面的法向量的模长来得到。曲面的法向量为 $\vec{n}=\nabla(x+y+z-3)=(1,1,1)$,其模长为 $\sqrt{1^2+1^2+1^2}=\sqrt{3}$。因此,$ds=\sqrt{3}dA$,其中 $dA$ 是在 $xy$ 平面上的微分面积元素。
步骤 3:计算曲面积分
曲面积分 $\iint xds$ 可以表示为 $\iint x\sqrt{3}dA$。在极坐标下,$dA=rdrd\theta$,因此积分变为 $\sqrt{3}\int_{0}^{2\pi}\int_{0}^{1}r\cos\theta r drd\theta$。计算这个积分,我们得到 $\sqrt{3}\int_{0}^{2\pi}\cos\theta d\theta\int_{0}^{1}r^2 dr$。由于 $\int_{0}^{2\pi}\cos\theta d\theta=0$,所以整个积分的结果为 $0$。
平面 $x+y+z=3$ 可以表示为 $z=3-x-y$。圆柱面 ${x}^{2}+{y}^{2}=1$ 表示 $x$ 和 $y$ 的范围。因此,我们可以使用极坐标参数化曲面,设 $x=r\cos\theta$,$y=r\sin\theta$,其中 $0\leq r\leq 1$,$0\leq\theta\leq 2\pi$。则 $z=3-r\cos\theta-r\sin\theta$。
步骤 2:计算曲面的微分面积元素 $ds$
曲面的微分面积元素 $ds$ 可以通过计算曲面的法向量的模长来得到。曲面的法向量为 $\vec{n}=\nabla(x+y+z-3)=(1,1,1)$,其模长为 $\sqrt{1^2+1^2+1^2}=\sqrt{3}$。因此,$ds=\sqrt{3}dA$,其中 $dA$ 是在 $xy$ 平面上的微分面积元素。
步骤 3:计算曲面积分
曲面积分 $\iint xds$ 可以表示为 $\iint x\sqrt{3}dA$。在极坐标下,$dA=rdrd\theta$,因此积分变为 $\sqrt{3}\int_{0}^{2\pi}\int_{0}^{1}r\cos\theta r drd\theta$。计算这个积分,我们得到 $\sqrt{3}\int_{0}^{2\pi}\cos\theta d\theta\int_{0}^{1}r^2 dr$。由于 $\int_{0}^{2\pi}\cos\theta d\theta=0$,所以整个积分的结果为 $0$。