题目
函数 =sin x+sqrt (3)cos x 的最小正周期是 ()-|||-A.2π B.π C. dfrac (2pi )(sqrt {3)} D. dfrac (pi )(6)
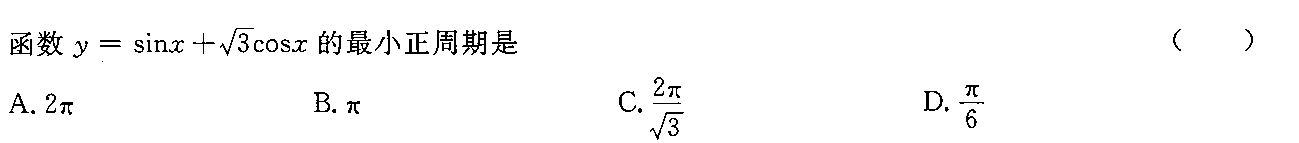
题目解答
答案
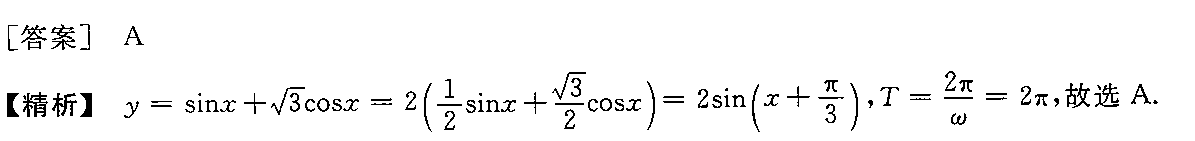
解析
步骤 1:将函数 $y=\sin x+\sqrt {3}\cos x$ 转换为标准形式
我们首先将给定的函数 $y=\sin x+\sqrt {3}\cos x$ 转换为标准形式,即 $y=A\sin (x+\phi)$ 的形式,其中 $A$ 是振幅,$\phi$ 是相位角。为此,我们需要找到一个合适的 $A$ 和 $\phi$,使得 $y=A\sin (x+\phi)$ 等价于 $y=\sin x+\sqrt {3}\cos x$。
步骤 2:确定振幅 $A$
振幅 $A$ 可以通过计算 $\sqrt{1^2+(\sqrt{3})^2}$ 得到,因为 $\sin x$ 和 $\sqrt{3}\cos x$ 的系数分别是 $1$ 和 $\sqrt{3}$。所以,$A=\sqrt{1^2+(\sqrt{3})^2}=\sqrt{1+3}=\sqrt{4}=2$。
步骤 3:确定相位角 $\phi$
相位角 $\phi$ 可以通过 $\tan \phi = \frac{\sqrt{3}}{1}$ 来确定,因为 $\sin x$ 和 $\sqrt{3}\cos x$ 的系数分别是 $1$ 和 $\sqrt{3}$。所以,$\phi=\arctan(\sqrt{3})=\frac{\pi}{3}$。
步骤 4:确定函数的最小正周期
函数 $y=A\sin (x+\phi)$ 的最小正周期是 $T=\frac{2\pi}{\omega}$,其中 $\omega$ 是角频率。在这个问题中,$\omega=1$,所以 $T=\frac{2\pi}{1}=2\pi$。
我们首先将给定的函数 $y=\sin x+\sqrt {3}\cos x$ 转换为标准形式,即 $y=A\sin (x+\phi)$ 的形式,其中 $A$ 是振幅,$\phi$ 是相位角。为此,我们需要找到一个合适的 $A$ 和 $\phi$,使得 $y=A\sin (x+\phi)$ 等价于 $y=\sin x+\sqrt {3}\cos x$。
步骤 2:确定振幅 $A$
振幅 $A$ 可以通过计算 $\sqrt{1^2+(\sqrt{3})^2}$ 得到,因为 $\sin x$ 和 $\sqrt{3}\cos x$ 的系数分别是 $1$ 和 $\sqrt{3}$。所以,$A=\sqrt{1^2+(\sqrt{3})^2}=\sqrt{1+3}=\sqrt{4}=2$。
步骤 3:确定相位角 $\phi$
相位角 $\phi$ 可以通过 $\tan \phi = \frac{\sqrt{3}}{1}$ 来确定,因为 $\sin x$ 和 $\sqrt{3}\cos x$ 的系数分别是 $1$ 和 $\sqrt{3}$。所以,$\phi=\arctan(\sqrt{3})=\frac{\pi}{3}$。
步骤 4:确定函数的最小正周期
函数 $y=A\sin (x+\phi)$ 的最小正周期是 $T=\frac{2\pi}{\omega}$,其中 $\omega$ 是角频率。在这个问题中,$\omega=1$,所以 $T=\frac{2\pi}{1}=2\pi$。