题目
设 为一单连通开区域, , 在 内具有一阶连续偏导数,则下列哪个条件与其他三个条件不等价() 任一封闭曲线积分 曲线积分在内与路径无关 为某一二元函数的全微分 在内恒成立
设 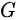 为一单连通开区域,
为一单连通开区域, 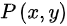 ,
,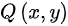 在
在 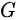 内具有一阶连续偏导数,则下列哪个条件与其他三个条件不等价()
内具有一阶连续偏导数,则下列哪个条件与其他三个条件不等价()
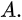 任一封闭曲线积分
任一封闭曲线积分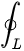
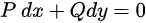
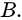 曲线积分
曲线积分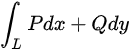 在
在 内与路径无关
内与路径无关
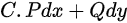 为某一二元函数的全微分
为某一二元函数的全微分
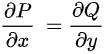 在
在 内恒成立
内恒成立
题目解答
答案
解:
若 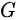 为一单连通开区域,
为一单连通开区域, 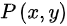 ,
,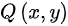 在
在 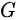 内具有一阶连续偏导,则任意封闭曲线积分均为
内具有一阶连续偏导,则任意封闭曲线积分均为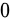 ,且与积分路径无关,即沿
,且与积分路径无关,即沿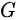 内任意闭曲线的曲线积分为零,但它的充分必要条件是
内任意闭曲线的曲线积分为零,但它的充分必要条件是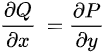 。并且
。并且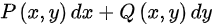 是在
是在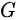 内二元函数
内二元函数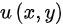 的全微分.因此选项
的全微分.因此选项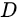 与其他三个条件不等价。故答案为
与其他三个条件不等价。故答案为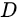 .
.
解析
步骤 1:理解单连通开区域和一阶连续偏导数
单连通开区域意味着在该区域内没有“洞”,即任意闭合曲线都可以连续地收缩到一个点。P(x,y)和Q(x,y)在该区域内具有一阶连续偏导数,意味着它们的偏导数在该区域内连续。
步骤 2:分析选项A
选项A表示在单连通开区域内,对于任意封闭曲线,Pdx+Qdy的积分等于0。这是格林定理的一个直接结果,当P和Q满足一定条件时,封闭曲线上的积分等于0。
步骤 3:分析选项B
选项B表示在单连通开区域内,曲线积分Pdx+Qdy与路径无关。这是格林定理的另一个结果,当P和Q满足一定条件时,积分结果与路径无关,只与起点和终点有关。
步骤 4:分析选项C
选项C表示Pdx+Qdy是某一二元函数的全微分。这是格林定理的又一个结果,当P和Q满足一定条件时,Pdx+Qdy可以表示为某一函数的全微分。
步骤 5:分析选项D
选项D表示$\dfrac {\partial P}{\partial x}=\dfrac {\partial Q}{\partial y}$在单连通开区域内恒成立。这是格林定理的条件之一,当P和Q满足这个条件时,格林定理成立。
步骤 6:确定不等价的条件
选项A、B、C都是格林定理的直接结果,而选项D是格林定理的条件之一。因此,选项D与其他三个条件不等价。
单连通开区域意味着在该区域内没有“洞”,即任意闭合曲线都可以连续地收缩到一个点。P(x,y)和Q(x,y)在该区域内具有一阶连续偏导数,意味着它们的偏导数在该区域内连续。
步骤 2:分析选项A
选项A表示在单连通开区域内,对于任意封闭曲线,Pdx+Qdy的积分等于0。这是格林定理的一个直接结果,当P和Q满足一定条件时,封闭曲线上的积分等于0。
步骤 3:分析选项B
选项B表示在单连通开区域内,曲线积分Pdx+Qdy与路径无关。这是格林定理的另一个结果,当P和Q满足一定条件时,积分结果与路径无关,只与起点和终点有关。
步骤 4:分析选项C
选项C表示Pdx+Qdy是某一二元函数的全微分。这是格林定理的又一个结果,当P和Q满足一定条件时,Pdx+Qdy可以表示为某一函数的全微分。
步骤 5:分析选项D
选项D表示$\dfrac {\partial P}{\partial x}=\dfrac {\partial Q}{\partial y}$在单连通开区域内恒成立。这是格林定理的条件之一,当P和Q满足这个条件时,格林定理成立。
步骤 6:确定不等价的条件
选项A、B、C都是格林定理的直接结果,而选项D是格林定理的条件之一。因此,选项D与其他三个条件不等价。