题目
求由曲线 y=x+2 和 =(x)^2 所围成的平面图形的面积.

题目解答
答案
解析
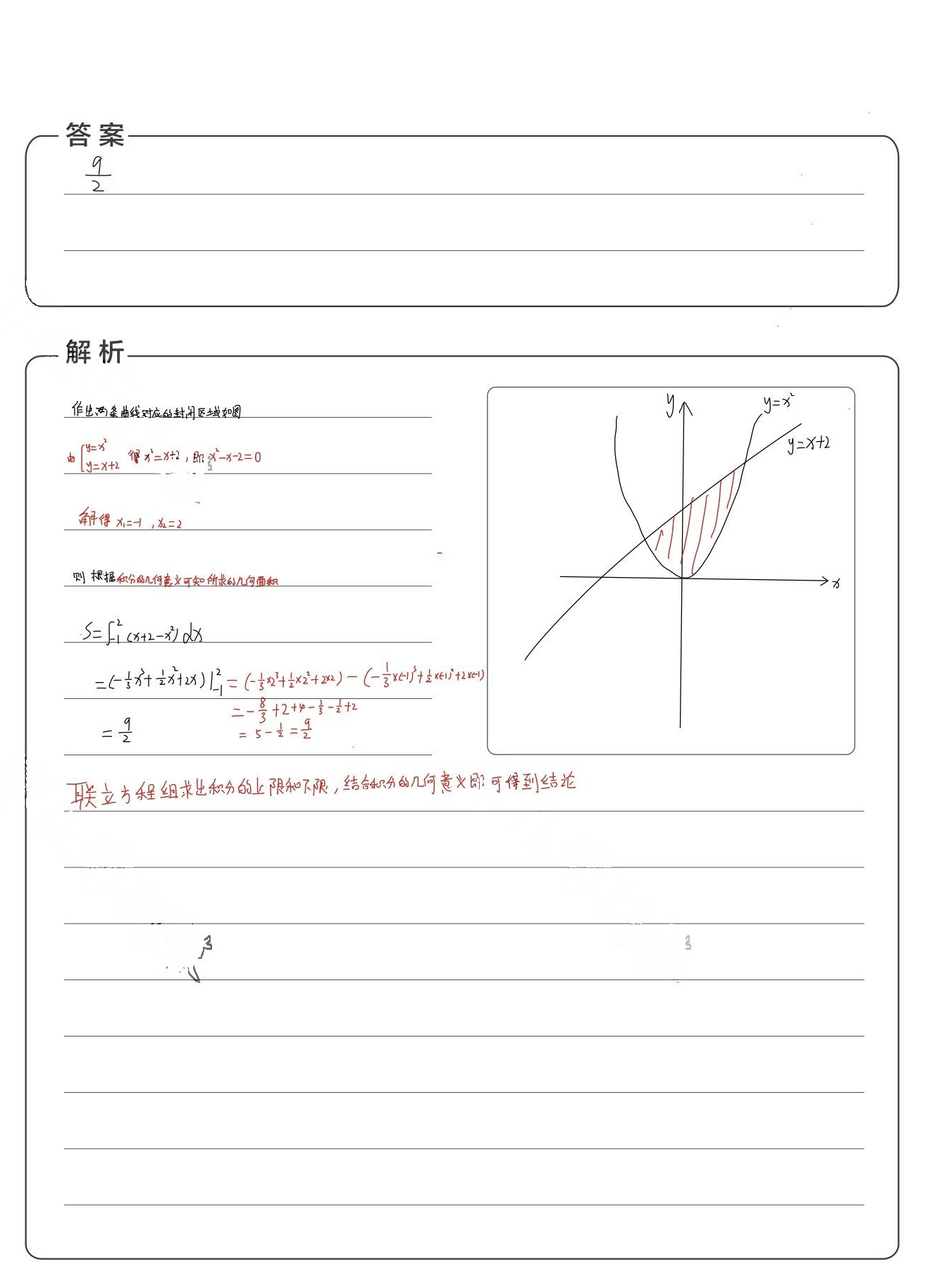
步骤 1:确定交点
为了确定曲线 $y=x+2$ 和 $y=x^2$ 的交点,我们需要解方程 $x+2=x^2$。这可以转化为 $x^2-x-2=0$。通过因式分解,我们得到 $(x-2)(x+1)=0$,从而得到 $x=2$ 和 $x=-1$ 作为交点的横坐标。
步骤 2:计算面积
为了计算由这两条曲线所围成的平面图形的面积,我们需要计算积分 $\int_{-1}^{2} (x+2-x^2) dx$。这个积分表示的是从 $x=-1$ 到 $x=2$ 的区间内,$y=x+2$ 和 $y=x^2$ 之间的区域的面积。
步骤 3:执行积分
计算积分 $\int_{-1}^{2} (x+2-x^2) dx$,我们得到:
$$
\int_{-1}^{2} (x+2-x^2) dx = \left[ \frac{1}{2}x^2 + 2x - \frac{1}{3}x^3 \right]_{-1}^{2}
$$
$$
= \left( \frac{1}{2}(2)^2 + 2(2) - \frac{1}{3}(2)^3 \right) - \left( \frac{1}{2}(-1)^2 + 2(-1) - \frac{1}{3}(-1)^3 \right)
$$
$$
= \left( 2 + 4 - \frac{8}{3} \right) - \left( \frac{1}{2} - 2 + \frac{1}{3} \right)
$$
$$
= \left( 6 - \frac{8}{3} \right) - \left( -\frac{3}{2} + \frac{1}{3} \right)
$$
$$
= \frac{18}{3} - \frac{8}{3} + \frac{9}{6} - \frac{2}{6}
$$
$$
= \frac{10}{3} + \frac{7}{6}
$$
$$
= \frac{20}{6} + \frac{7}{6}
$$
$$
= \frac{27}{6}
$$
$$
= \frac{9}{2}
$$
为了确定曲线 $y=x+2$ 和 $y=x^2$ 的交点,我们需要解方程 $x+2=x^2$。这可以转化为 $x^2-x-2=0$。通过因式分解,我们得到 $(x-2)(x+1)=0$,从而得到 $x=2$ 和 $x=-1$ 作为交点的横坐标。
步骤 2:计算面积
为了计算由这两条曲线所围成的平面图形的面积,我们需要计算积分 $\int_{-1}^{2} (x+2-x^2) dx$。这个积分表示的是从 $x=-1$ 到 $x=2$ 的区间内,$y=x+2$ 和 $y=x^2$ 之间的区域的面积。
步骤 3:执行积分
计算积分 $\int_{-1}^{2} (x+2-x^2) dx$,我们得到:
$$
\int_{-1}^{2} (x+2-x^2) dx = \left[ \frac{1}{2}x^2 + 2x - \frac{1}{3}x^3 \right]_{-1}^{2}
$$
$$
= \left( \frac{1}{2}(2)^2 + 2(2) - \frac{1}{3}(2)^3 \right) - \left( \frac{1}{2}(-1)^2 + 2(-1) - \frac{1}{3}(-1)^3 \right)
$$
$$
= \left( 2 + 4 - \frac{8}{3} \right) - \left( \frac{1}{2} - 2 + \frac{1}{3} \right)
$$
$$
= \left( 6 - \frac{8}{3} \right) - \left( -\frac{3}{2} + \frac{1}{3} \right)
$$
$$
= \frac{18}{3} - \frac{8}{3} + \frac{9}{6} - \frac{2}{6}
$$
$$
= \frac{10}{3} + \frac{7}{6}
$$
$$
= \frac{20}{6} + \frac{7}{6}
$$
$$
= \frac{27}{6}
$$
$$
= \frac{9}{2}
$$