题目
圆柱体上底的中心到下底的边沿的距离为d,问当底半径与高分别为多少时,圆柱体的体积最大?
圆柱体上底的中心到下底的边沿的距离为d,问当底半径与高分别为多少
时,圆柱体的体积最大?
题目解答
答案
解: 如图所示,圆柱体高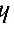
与底半径
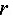满足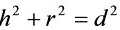
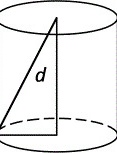圆柱体的体积公式为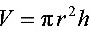
将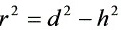
代入得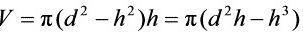
求导得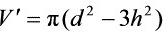
令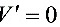
,解得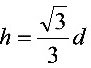
是唯一驻点,由于
经过驻点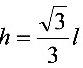
时,符号是由正变负,所以该驻点是实际问题的最大值点;由此出
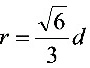.所以当底半径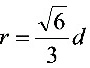,高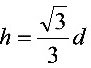时,圆柱体的体积最大.
解析
步骤 1：建立圆柱体的体积公式
圆柱体的体积公式为$V=\pi {r}^{2}h$，其中$r$是底半径，$h$是高。
步骤 2：利用已知条件建立关系式
根据题意，圆柱体上底的中心到下底的边沿的距离为$d$，可以得到${h}^{2}+{r}^{2}={d}^{2}$。
步骤 3：将关系式代入体积公式
将${r}^{2}={d}^{2}-{h}^{2}$代入体积公式$V=\pi {r}^{2}h$，得到$V=\pi ({d}^{2}-{h}^{2})h=\pi ({d}^{2}h-{h}^{3})$。
步骤 4：求导并求极值
对$V$关于$h$求导，得到$V'=\pi ({d}^{2}-3{h}^{2})$。令$V'=0$，解得$h=\dfrac {\sqrt {3}}{3}d$。由于经过驻点$h=\dfrac {\sqrt {3}}{3}d$时，$V'$的符号由正变负，所以该驻点是实际问题的最大值点。
步骤 5：计算底半径
将$h=\dfrac {\sqrt {3}}{3}d$代入${r}^{2}={d}^{2}-{h}^{2}$，得到$r=\dfrac {\sqrt {6}}{3}d$。
圆柱体的体积公式为$V=\pi {r}^{2}h$，其中$r$是底半径，$h$是高。
步骤 2：利用已知条件建立关系式
根据题意，圆柱体上底的中心到下底的边沿的距离为$d$，可以得到${h}^{2}+{r}^{2}={d}^{2}$。
步骤 3：将关系式代入体积公式
将${r}^{2}={d}^{2}-{h}^{2}$代入体积公式$V=\pi {r}^{2}h$，得到$V=\pi ({d}^{2}-{h}^{2})h=\pi ({d}^{2}h-{h}^{3})$。
步骤 4：求导并求极值
对$V$关于$h$求导，得到$V'=\pi ({d}^{2}-3{h}^{2})$。令$V'=0$，解得$h=\dfrac {\sqrt {3}}{3}d$。由于经过驻点$h=\dfrac {\sqrt {3}}{3}d$时，$V'$的符号由正变负，所以该驻点是实际问题的最大值点。
步骤 5：计算底半径
将$h=\dfrac {\sqrt {3}}{3}d$代入${r}^{2}={d}^{2}-{h}^{2}$，得到$r=\dfrac {\sqrt {6}}{3}d$。