题目
4.证明:(1) lim _((x,y)arrow (0,0))dfrac (x+y)(x-y) 不存在;(2)-|||-lim _((x,y)arrow (0,0))(x)(x) 不存在.
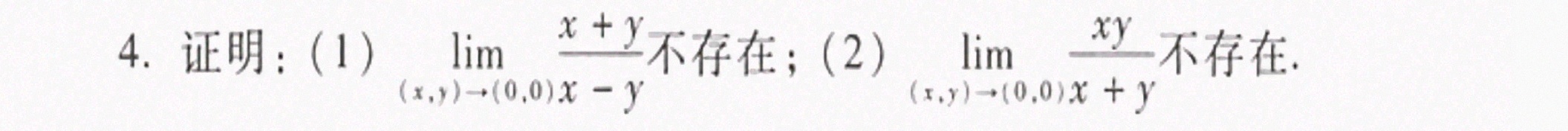
题目解答
答案
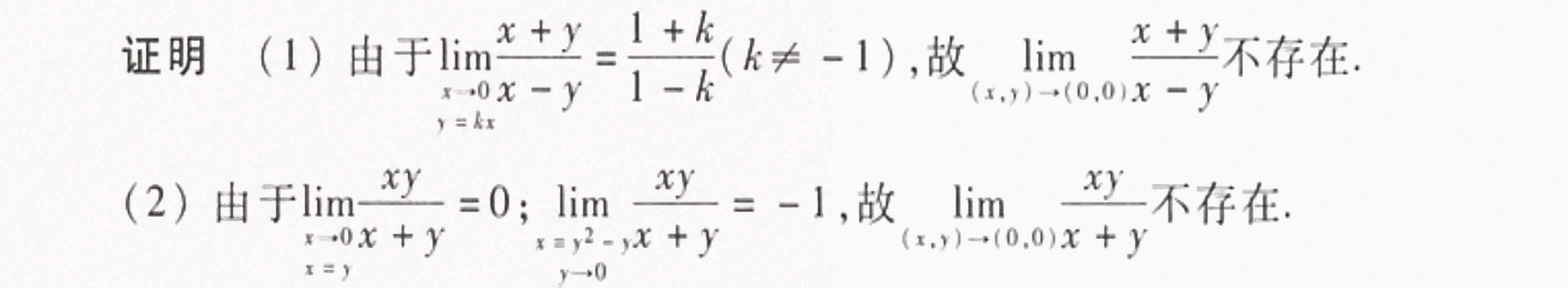
解析
步骤 1:考虑路径 $y = kx$
对于路径 $y = kx$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {x+y}{x-y}=\lim _{x\rightarrow 0}\dfrac {x+kx}{x-kx}=\lim _{x\rightarrow 0}\dfrac {1+k}{1-k}$$
步骤 2:分析极限值
由于 $\lim _{x\rightarrow 0}\dfrac {x+y}{x-y}=\dfrac {1+k}{1-k}$,这个极限值依赖于 $k$ 的值,因此当 $k$ 不同时,极限值不同,这表明极限不存在。
步骤 3:考虑路径 $y = x^2$
对于路径 $y = x^2$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {xy}{x+y}=\lim _{x\rightarrow 0}\dfrac {x^3}{x+x^2}=\lim _{x\rightarrow 0}\dfrac {x^2}{1+x}=0$$
步骤 4:考虑路径 $y = x$
对于路径 $y = x$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {xy}{x+y}=\lim _{x\rightarrow 0}\dfrac {x^2}{2x}=\lim _{x\rightarrow 0}\dfrac {x}{2}=-1$$
步骤 5:分析极限值
由于 $\lim _{x\rightarrow 0}\dfrac {xy}{x+y}$ 在路径 $y = x^2$ 和 $y = x$ 上的极限值不同,这表明极限不存在。
对于路径 $y = kx$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {x+y}{x-y}=\lim _{x\rightarrow 0}\dfrac {x+kx}{x-kx}=\lim _{x\rightarrow 0}\dfrac {1+k}{1-k}$$
步骤 2:分析极限值
由于 $\lim _{x\rightarrow 0}\dfrac {x+y}{x-y}=\dfrac {1+k}{1-k}$,这个极限值依赖于 $k$ 的值,因此当 $k$ 不同时,极限值不同,这表明极限不存在。
步骤 3:考虑路径 $y = x^2$
对于路径 $y = x^2$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {xy}{x+y}=\lim _{x\rightarrow 0}\dfrac {x^3}{x+x^2}=\lim _{x\rightarrow 0}\dfrac {x^2}{1+x}=0$$
步骤 4:考虑路径 $y = x$
对于路径 $y = x$,我们有:
$$\lim _{x\rightarrow 0}\dfrac {xy}{x+y}=\lim _{x\rightarrow 0}\dfrac {x^2}{2x}=\lim _{x\rightarrow 0}\dfrac {x}{2}=-1$$
步骤 5:分析极限值
由于 $\lim _{x\rightarrow 0}\dfrac {xy}{x+y}$ 在路径 $y = x^2$ 和 $y = x$ 上的极限值不同,这表明极限不存在。