题目
8.求直线 ) 2x+3y-z-4=0 3x-5y+2z+1=0 . 的标准式方程和参数方程.
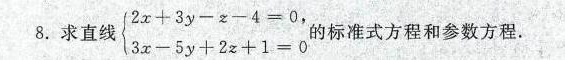
题目解答
答案
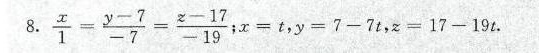
解析
步骤 1:求解直线的方向向量
为了找到直线的方向向量,我们需要计算两个平面的法向量的叉积。给定的平面方程为:
$$
\begin{cases}
2x + 3y - z - 4 = 0 \\
3x - 5y + 2z + 1 = 0
\end{cases}
$$
平面的法向量分别为 $\vec{n_1} = (2, 3, -1)$ 和 $\vec{n_2} = (3, -5, 2)$。直线的方向向量 $\vec{d}$ 可以通过 $\vec{n_1}$ 和 $\vec{n_2}$ 的叉积得到:
$$
\vec{d} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix}
\vec{i} & \vec{j} & \vec{k} \\
2 & 3 & -1 \\
3 & -5 & 2
\end{vmatrix} = (3 \cdot 2 - (-1) \cdot (-5))\vec{i} - (2 \cdot 2 - (-1) \cdot 3)\vec{j} + (2 \cdot (-5) - 3 \cdot 3)\vec{k} = (6 - 5)\vec{i} - (4 + 3)\vec{j} + (-10 - 9)\vec{k} = \vec{i} - 7\vec{j} - 19\vec{k}
$$
因此,直线的方向向量为 $\vec{d} = (1, -7, -19)$。
步骤 2:求解直线上的一个点
为了找到直线上的一个点,我们可以选择一个特定的 $x$ 值,然后解出对应的 $y$ 和 $z$ 值。例如,令 $x = 0$,代入两个平面方程中,得到:
$$
\begin{cases}
3y - z - 4 = 0 \\
-5y + 2z + 1 = 0
\end{cases}
$$
解这个方程组,得到:
$$
\begin{cases}
3y - z = 4 \\
-5y + 2z = -1
\end{cases}
$$
将第一个方程乘以2,得到:
$$
\begin{cases}
6y - 2z = 8 \\
-5y + 2z = -1
\end{cases}
$$
将两个方程相加,得到:
$$
y = 7
$$
将 $y = 7$ 代入 $3y - z = 4$,得到:
$$
z = 17
$$
因此,直线上的一个点为 $(0, 7, 17)$。
步骤 3:写出直线的标准式方程和参数方程
根据直线的方向向量和直线上的一个点,可以写出直线的标准式方程和参数方程。标准式方程为:
$$
\dfrac{x - 0}{1} = \dfrac{y - 7}{-7} = \dfrac{z - 17}{-19}
$$
参数方程为:
$$
\begin{cases}
x = t \\
y = 7 - 7t \\
z = 17 - 19t
\end{cases}
$$
为了找到直线的方向向量,我们需要计算两个平面的法向量的叉积。给定的平面方程为:
$$
\begin{cases}
2x + 3y - z - 4 = 0 \\
3x - 5y + 2z + 1 = 0
\end{cases}
$$
平面的法向量分别为 $\vec{n_1} = (2, 3, -1)$ 和 $\vec{n_2} = (3, -5, 2)$。直线的方向向量 $\vec{d}$ 可以通过 $\vec{n_1}$ 和 $\vec{n_2}$ 的叉积得到:
$$
\vec{d} = \vec{n_1} \times \vec{n_2} = \begin{vmatrix}
\vec{i} & \vec{j} & \vec{k} \\
2 & 3 & -1 \\
3 & -5 & 2
\end{vmatrix} = (3 \cdot 2 - (-1) \cdot (-5))\vec{i} - (2 \cdot 2 - (-1) \cdot 3)\vec{j} + (2 \cdot (-5) - 3 \cdot 3)\vec{k} = (6 - 5)\vec{i} - (4 + 3)\vec{j} + (-10 - 9)\vec{k} = \vec{i} - 7\vec{j} - 19\vec{k}
$$
因此,直线的方向向量为 $\vec{d} = (1, -7, -19)$。
步骤 2:求解直线上的一个点
为了找到直线上的一个点,我们可以选择一个特定的 $x$ 值,然后解出对应的 $y$ 和 $z$ 值。例如,令 $x = 0$,代入两个平面方程中,得到:
$$
\begin{cases}
3y - z - 4 = 0 \\
-5y + 2z + 1 = 0
\end{cases}
$$
解这个方程组,得到:
$$
\begin{cases}
3y - z = 4 \\
-5y + 2z = -1
\end{cases}
$$
将第一个方程乘以2,得到:
$$
\begin{cases}
6y - 2z = 8 \\
-5y + 2z = -1
\end{cases}
$$
将两个方程相加,得到:
$$
y = 7
$$
将 $y = 7$ 代入 $3y - z = 4$,得到:
$$
z = 17
$$
因此,直线上的一个点为 $(0, 7, 17)$。
步骤 3:写出直线的标准式方程和参数方程
根据直线的方向向量和直线上的一个点,可以写出直线的标准式方程和参数方程。标准式方程为:
$$
\dfrac{x - 0}{1} = \dfrac{y - 7}{-7} = \dfrac{z - 17}{-19}
$$
参数方程为:
$$
\begin{cases}
x = t \\
y = 7 - 7t \\
z = 17 - 19t
\end{cases}
$$