求 (int )_(0)^8dfrac (1)(1+sqrt [3]{x)}dx
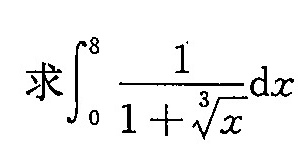
题目解答
答案
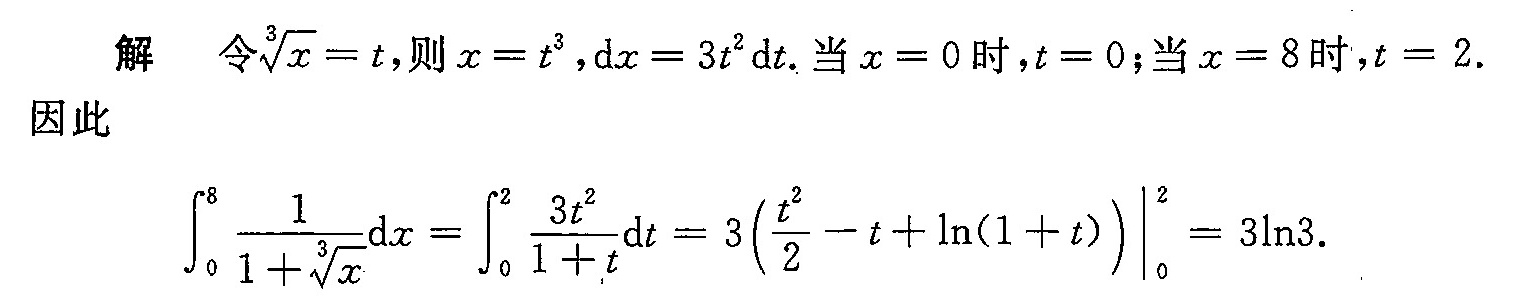
解析
考查要点:本题主要考查定积分的计算,特别是通过变量替换法简化积分表达式的能力,以及对分式函数积分技巧的掌握。
解题核心思路:
- 变量替换:令 $\sqrt[3]{x} = t$,将原积分转化为关于 $t$ 的积分,简化被积函数。
- 分式分解:将被积函数 $\frac{t^2}{1+t}$ 分解为多项式与简单分式的组合,便于逐项积分。
- 逐项积分:分别计算多项式部分和分式部分的积分,最后代入上下限求解。
破题关键点:
- 正确选择替换变量,明确替换后的积分上下限。
- 灵活分解被积函数,避免直接展开带来的复杂计算。
变量替换:
令 $\sqrt[3]{x} = t$,则 $x = t^3$,$dx = 3t^2 dt$。
当 $x = 0$ 时,$t = 0$;当 $x = 8$ 时,$t = 2$。
原积分变为:
$\int_{0}^{8} \frac{1}{1+\sqrt[3]{x}} dx = \int_{0}^{2} \frac{1}{1+t} \cdot 3t^2 dt = 3 \int_{0}^{2} \frac{t^2}{1+t} dt.$
分式分解:
将 $\frac{t^2}{1+t}$ 分解为多项式与简单分式:
$\frac{t^2}{1+t} = t - 1 + \frac{1}{1+t}.$
逐项积分:
$3 \int_{0}^{2} \left( t - 1 + \frac{1}{1+t} \right) dt = 3 \left[ \int_{0}^{2} (t - 1) dt + \int_{0}^{2} \frac{1}{1+t} dt \right].$
-
计算多项式部分:
$\int_{0}^{2} (t - 1) dt = \left[ \frac{1}{2}t^2 - t \right]_{0}^{2} = \left( \frac{1}{2}(2)^2 - 2 \right) - \left( 0 - 0 \right) = 0.$ -
计算分式部分:
$\int_{0}^{2} \frac{1}{1+t} dt = \left[ \ln|1+t| \right]_{0}^{2} = \ln3 - \ln1 = \ln3.$
综合结果:
$3 \left( 0 + \ln3 \right) = 3\ln3.$