题目
求内接于半径为sqrt (3)的球且有最大体积的长方体的长、宽、高分别是多少
求内接于半径为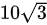
的球且有最大体积的长方体的长、宽、高分别是多少
题目解答
答案
依题意，设
长方体的长为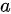
，宽为
，高为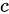
∴
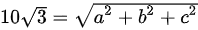
即，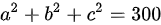
∴长方体体积为：
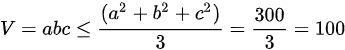
当且仅当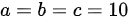
时，取等号，此时长方体即为正方体
∴长方体的长，宽，高分别为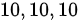
解析
步骤 1：设定长方体的长、宽、高
设长方体的长为$a$，宽为$b$，高为$c$。
步骤 2：利用球的半径和长方体的对角线关系
由于长方体的对角线是球的直径，所以有：
$10\sqrt {3}=\sqrt {{a}^{2}+{b}^{2}+{c}^{2}}$
步骤 3：求长方体体积的最大值
长方体的体积$V=abc$，根据步骤2中的关系，有：
${a}^{2}+{b}^{2}+{c}^{2}=300$
根据均值不等式，有：
$abc\leqslant \dfrac {({a}^{2}+{b}^{2}+{c}^{2})}{3}=\dfrac {300}{3}=100$
当且仅当$a=b=c=10$时，取等号，此时长方体即为正方体。
设长方体的长为$a$，宽为$b$，高为$c$。
步骤 2：利用球的半径和长方体的对角线关系
由于长方体的对角线是球的直径，所以有：
$10\sqrt {3}=\sqrt {{a}^{2}+{b}^{2}+{c}^{2}}$
步骤 3：求长方体体积的最大值
长方体的体积$V=abc$，根据步骤2中的关系，有：
${a}^{2}+{b}^{2}+{c}^{2}=300$
根据均值不等式，有：
$abc\leqslant \dfrac {({a}^{2}+{b}^{2}+{c}^{2})}{3}=\dfrac {300}{3}=100$
当且仅当$a=b=c=10$时，取等号，此时长方体即为正方体。