题目
2.设a是常数,则当函数 (x)=asin x+dfrac (1)(3)sin 3x 在 =dfrac (pi )(3) 处取得极值时,必有 a=-|||-(A)0. (B)1. (C)2. (D)3.
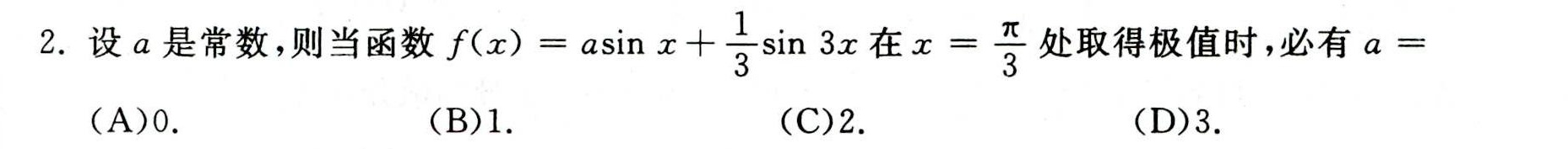
题目解答
答案

解析
步骤 1:求导数
首先,我们需要求出函数 $f(x)=a\sin x+\dfrac {1}{3}\sin 3x$ 的导数 $f'(x)$。根据导数的求导法则,我们有:
$$f'(x) = a\cos x + \cos 3x$$
步骤 2:求驻点
函数在 $x=\dfrac {\pi }{3}$ 处取得极值,说明该点是函数的驻点,即 $f'(\dfrac {\pi }{3})=0$。将 $x=\dfrac {\pi }{3}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\dfrac {\pi }{3}) = a\cos \dfrac {\pi }{3} + \cos \dfrac {3\pi }{3} = \dfrac {a}{2} - 1$$
步骤 3:求解a
由于 $f'(\dfrac {\pi }{3})=0$,我们有:
$$\dfrac {a}{2} - 1 = 0$$
解得:
$$a = 2$$
首先,我们需要求出函数 $f(x)=a\sin x+\dfrac {1}{3}\sin 3x$ 的导数 $f'(x)$。根据导数的求导法则,我们有:
$$f'(x) = a\cos x + \cos 3x$$
步骤 2:求驻点
函数在 $x=\dfrac {\pi }{3}$ 处取得极值,说明该点是函数的驻点,即 $f'(\dfrac {\pi }{3})=0$。将 $x=\dfrac {\pi }{3}$ 代入导数 $f'(x)$ 中,得到:
$$f'(\dfrac {\pi }{3}) = a\cos \dfrac {\pi }{3} + \cos \dfrac {3\pi }{3} = \dfrac {a}{2} - 1$$
步骤 3:求解a
由于 $f'(\dfrac {\pi }{3})=0$,我们有:
$$\dfrac {a}{2} - 1 = 0$$
解得:
$$a = 2$$