题目
求极限lim _(xarrow +infty )(({x)^dfrac (1{x)}-1)}^dfrac (1{ln x)}.
求极限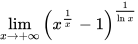 .
.
题目解答
答案
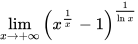

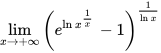
=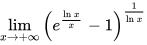

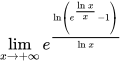
∵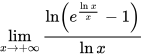

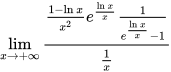

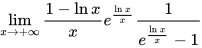

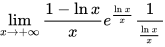

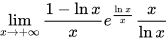

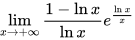
=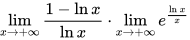

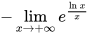

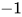
∴原式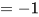
故答案为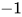
解析
步骤 1:将原式转换为指数形式
原式可以写成$\lim _{x\rightarrow +\infty }{({e}^{\ln {x}^{\dfrac {1}{x}}}-1)}^{\dfrac {1}{\ln x}}$,因为$x^{\frac{1}{x}}$可以写成$e^{\ln x^{\frac{1}{x}}}$。
步骤 2:简化指数部分
$\lim _{x\rightarrow +\infty }{({e}^{\dfrac {\ln x}{x}}-1)}^{\dfrac {1}{\ln x}}$,因为$\ln x^{\frac{1}{x}} = \frac{\ln x}{x}$。
步骤 3:利用对数的性质
$\lim _{x\rightarrow +\infty }\dfrac {\ln ({e}^{\dfrac {\ln x}{x}}-1)}{\ln x}$,将指数部分的对数提取出来。
步骤 4:应用洛必达法则
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{x}{e}^{\dfrac {\ln x}{x}}\dfrac {1}{\dfrac {\ln x}{x}}$,对分子分母同时求导。
步骤 5:进一步简化
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}{e}^{\dfrac {\ln x}{x}}$,将分母中的$x$与$\ln x$约去。
步骤 6:计算极限
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}\cdot \lim _{x\rightarrow +\infty }{e}^{\dfrac {\ln x}{x}}$,将极限分成两部分计算。
步骤 7:得出结论
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}=-1$,$\lim _{x\rightarrow +\infty }{e}^{\dfrac {\ln x}{x}}=1$,所以原式=-1。
原式可以写成$\lim _{x\rightarrow +\infty }{({e}^{\ln {x}^{\dfrac {1}{x}}}-1)}^{\dfrac {1}{\ln x}}$,因为$x^{\frac{1}{x}}$可以写成$e^{\ln x^{\frac{1}{x}}}$。
步骤 2:简化指数部分
$\lim _{x\rightarrow +\infty }{({e}^{\dfrac {\ln x}{x}}-1)}^{\dfrac {1}{\ln x}}$,因为$\ln x^{\frac{1}{x}} = \frac{\ln x}{x}$。
步骤 3:利用对数的性质
$\lim _{x\rightarrow +\infty }\dfrac {\ln ({e}^{\dfrac {\ln x}{x}}-1)}{\ln x}$,将指数部分的对数提取出来。
步骤 4:应用洛必达法则
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{x}{e}^{\dfrac {\ln x}{x}}\dfrac {1}{\dfrac {\ln x}{x}}$,对分子分母同时求导。
步骤 5:进一步简化
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}{e}^{\dfrac {\ln x}{x}}$,将分母中的$x$与$\ln x$约去。
步骤 6:计算极限
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}\cdot \lim _{x\rightarrow +\infty }{e}^{\dfrac {\ln x}{x}}$,将极限分成两部分计算。
步骤 7:得出结论
$\lim _{x\rightarrow +\infty }\dfrac {1-\ln x}{\ln x}=-1$,$\lim _{x\rightarrow +\infty }{e}^{\dfrac {\ln x}{x}}=1$,所以原式=-1。