题目
lim _(xarrow 0)dfrac ({(1+2{x)^2)}^dfrac (3{2)}-1}(tan 2x(cos sqrt {x)-1)}。
。
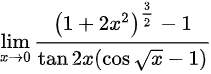题目解答
答案
当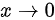
，有
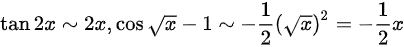，所以利用等价无穷小替换有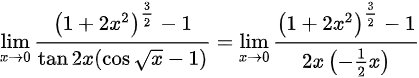
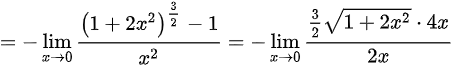
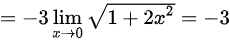，故答案为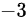
解析
步骤 1：等价无穷小替换
当$x\rightarrow 0$时，$\tan 2x\sim 2x$，$\cos \sqrt {x}-1\sim -\dfrac {1}{2}{(\sqrt {x})}^{2}=-\dfrac {1}{2}x$。利用这些等价无穷小替换，可以简化原极限表达式。
步骤 2：替换并简化
将等价无穷小替换应用到原极限表达式中，得到$\lim _{x\rightarrow 0}\dfrac {{(1+2{x}^{2})}^{\dfrac {3}{2}}-1}{2x(-\dfrac {1}{2}x)}$，进一步简化为$\lim _{x\rightarrow 0}\dfrac {{(1+2{x}^{2})}^{\dfrac {3}{2}}-1}{{x}^{2}}$。
步骤 3：洛必达法则
由于分子和分母在$x\rightarrow 0$时都趋于0，可以应用洛必达法则，即对分子和分母分别求导，得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {3}{2}\sqrt {1+2{x}^{2}}\cdot 4x}{2x}$。
步骤 4：计算极限
计算得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {3}{2}\sqrt {1+2{x}^{2}}\cdot 4x}{2x}=-3\lim _{x\rightarrow 0}\sqrt {1+2{x}^{2}}=-3$。
当$x\rightarrow 0$时，$\tan 2x\sim 2x$，$\cos \sqrt {x}-1\sim -\dfrac {1}{2}{(\sqrt {x})}^{2}=-\dfrac {1}{2}x$。利用这些等价无穷小替换，可以简化原极限表达式。
步骤 2：替换并简化
将等价无穷小替换应用到原极限表达式中，得到$\lim _{x\rightarrow 0}\dfrac {{(1+2{x}^{2})}^{\dfrac {3}{2}}-1}{2x(-\dfrac {1}{2}x)}$，进一步简化为$\lim _{x\rightarrow 0}\dfrac {{(1+2{x}^{2})}^{\dfrac {3}{2}}-1}{{x}^{2}}$。
步骤 3：洛必达法则
由于分子和分母在$x\rightarrow 0$时都趋于0，可以应用洛必达法则，即对分子和分母分别求导，得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {3}{2}\sqrt {1+2{x}^{2}}\cdot 4x}{2x}$。
步骤 4：计算极限
计算得到$\lim _{x\rightarrow 0}\dfrac {\dfrac {3}{2}\sqrt {1+2{x}^{2}}\cdot 4x}{2x}=-3\lim _{x\rightarrow 0}\sqrt {1+2{x}^{2}}=-3$。